题目内容
16.若关于x的分式方程$\frac{k-1}{x+1}$=2的解为负数,则k的取值范围为k<3且k≠1.分析 分式方程去分母转化为整式方程,表示出整式方程的解,根据解为负数确定出k的范围即可.
解答 解:去分母得:k-1=2x+2,
解得:x=$\frac{k-3}{2}$,
由分式方程的解为负数,得到$\frac{k-3}{2}$<0,且x+1≠0,即$\frac{k-3}{2}$≠-1,
解得:k<3且k≠1,
故答案为:k<3且k≠1
点评 此题考查了分式方程的解,以及解一元一次不等式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
4.已知反比例函数y=$\frac{k}{x}$的图象过点A(1,-2),则k的值为( )
| A. | 1 | B. | 2 | C. | -2 | D. | -1 |
11.下列实数中最大的数是( )
| A. | 3 | B. | 0 | C. | $\sqrt{2}$ | D. | -4 |
1.某交警在一个路口统计的某时段来往车辆的车速情况如表:
则上述车速的中位数和众数分别是( )
| 车速(km/h) | 48 | 49 | 50 | 51 | 52 |
| 车辆数(辆) | 5 | 4 | 8 | 2 | 1 |
| A. | 50,8 | B. | 50,50 | C. | 49,50 | D. | 49,8 |
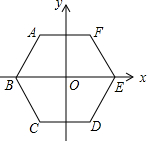 如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°.当n=2017时,顶点A的坐标为(2,2$\sqrt{3}$).
如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°.当n=2017时,顶点A的坐标为(2,2$\sqrt{3}$).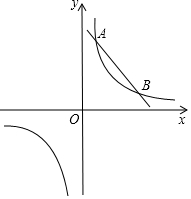 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图形交于A(a,4)和B(4,1)两点.
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图形交于A(a,4)和B(4,1)两点.