题目内容
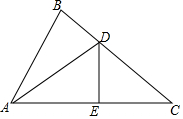
11.如图,线段AB,AD交于点A.C为直线AD上一点(不与点A,D重合).过点C在BC的右侧作射线CE⊥BC,过点D作直线DF∥AB,交CE于点G(G与D不重合).(1)如图1,若点C在线段AD上,且∠BCA为钝角.
①按要求补全图形;
②判断∠B与∠CGD的数量关系,并证明.
(2)若点C在线段DA的延长线上,请直接写出∠B与∠CGD的数量关系.
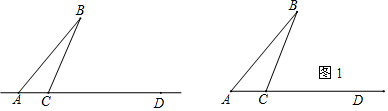
分析 (1)①依据过点C在BC的右侧作射线CE⊥BC,过点D作直线DF∥AB,交CE于点G,画出图形即可;②根据平行线的性质即可得到∠1=∠B,再根据平行线的性质,即可得出∠2+∠HCG=180°,进而得出∠CGD-∠B=90°.
(2)过点C作CH∥AB,根据平行线的性质可得∠B=∠BCH,再根据平行线的性质即可得到∠CGD+∠HCG=180°,进而得出∠B+∠CGD=90°.
解答 解:(1)①补全图形如图: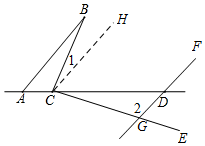
②判断:∠CGD-∠B=90°.
证明:过点C作CH∥AB,
∴∠1=∠B(两直线平行,内错角相等).
∵AB∥DF(已知),
∴CH∥DF(平行于同一直线的两直线平行).
∴∠2+∠HCG=180°(两直线平行,同旁内角互补).
∵CE⊥BC(已知),
∴∠1+∠HCG=90°(垂直的定义).
∴∠CGD+(90°-∠B)=180°,
即∠CGD-∠B=90°.
(2)∠CGD+∠B=90°.
理由:如图,过点C作CH∥AB,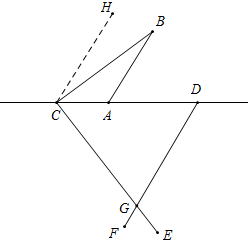
∴∠B=∠BCH,
∵AB∥DF(已知),
∴CH∥DF(平行于同一直线的两直线平行).
∴∠CGD+∠HCG=180°,
又∵CE⊥CB,
∴∠BCG=90°,
∴∠BCH+90°+∠CGD=180°,
即∠B+∠CGD=90°.
点评 本题主要考查了平行线的性质的运用,解题时注意:两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目
1.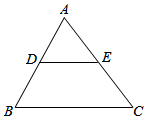 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=70°,∠B=70°,∠AED=30°,则∠C的度数是( )
如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=70°,∠B=70°,∠AED=30°,则∠C的度数是( )
 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=70°,∠B=70°,∠AED=30°,则∠C的度数是( )
如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=70°,∠B=70°,∠AED=30°,则∠C的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
6.下列调查中,最适合采用全面调查(普查)的是( )
| A. | 了解一批IPAD的使用寿命 | |
| B. | 了解某鱼塘中鱼的数量 | |
| C. | 了解某班学生对国家“一带一路”战略的知晓率 | |
| D. | 了解电视栏目《朗读者》的收视率 |
3.下列数字中,属于最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{2}{3}}$ | C. | $\sqrt{7}$ | D. | $\sqrt{0.3}$ |
20.下列事件是必然事件的是( )
| A. | 经过不断的努力,每个人都能获得“星光大道”年度总冠军 | |
| B. | 小冉打开电视,正在播放“奔跑吧,兄弟” | |
| C. | 火车开到月球上 | |
| D. | 在十三名中国学生中,必有属相相同的 |
1.下列运算正确的是( )
| A. | (ab)2=a2b2 | B. | a2+a4=a6 | C. | (a2)3=a5 | D. | a2•a3=a6 |
 如图,已知∠BAC=60°,∠B=80°,DE垂直平分AC交BC于点D,交AC于E.
如图,已知∠BAC=60°,∠B=80°,DE垂直平分AC交BC于点D,交AC于E.