题目内容
如图1,平面直角坐标系中,抛物线 与
与 轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与
轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与 轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.

(1)若点F的坐标为( ,
, ),AF=
),AF= .
.
①求此抛物线的解析式;
②点P是此抛物线上一个动点,点Q在此抛物线的对称轴上,以点A、F、P、Q为顶点构成的四边形是平行四边形,请直接写出点Q的坐标;
(2)若 ,
, ,且AB的长为
,且AB的长为 ,其中
,其中 .如图2,当∠DAF=45时,求
.如图2,当∠DAF=45时,求 的值和∠DFA的正切值.
的值和∠DFA的正切值.
 与
与 轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与
轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与 轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
(1)若点F的坐标为(
 ,
, ),AF=
),AF= .
.①求此抛物线的解析式;
②点P是此抛物线上一个动点,点Q在此抛物线的对称轴上,以点A、F、P、Q为顶点构成的四边形是平行四边形,请直接写出点Q的坐标;
(2)若
 ,
, ,且AB的长为
,且AB的长为 ,其中
,其中 .如图2,当∠DAF=45时,求
.如图2,当∠DAF=45时,求 的值和∠DFA的正切值.
的值和∠DFA的正切值.
(1)y= x2-
x2- x+
x+ Q1(
Q1( ,3) Q2(
,3) Q2( ,5) Q3(
,5) Q3( ,7)
,7)
 x2-
x2- x+
x+ Q1(
Q1( ,3) Q2(
,3) Q2( ,5) Q3(
,5) Q3( ,7)
,7)
试题分析(1):由题意。根据勾股定理易得到,点A B的坐标,将点代入解析式中求出b c 的值,因为对称轴x=
 ,所以,设Q(
,所以,设Q( ,n) P(m,
,n) P(m, m2+
m2+ m+
m+ ),∵QP//AF.且QP="AF.∴AF与PQ的斜率相同,即解析式中的k相等,将点A" F的坐标代人y=kx+b中得到AF的解析式,即可以得到PQ的解析式,含有m,n的方程,解得Q的坐标值。(2)问,做辅助线,过点D做DM//X轴,交抛物线与M,过点A做AH⊥Y轴,得到矩形,由此证得△ABF≌△AHM,及△AFD≌△AMD,得,∠DFA=∠AFB由于C为中点,∴DG=CB=HD=t,设DF=x,∴DF2=DG2+GF2∴(t+x)2=t2+(2t-x)2 解得x =
),∵QP//AF.且QP="AF.∴AF与PQ的斜率相同,即解析式中的k相等,将点A" F的坐标代人y=kx+b中得到AF的解析式,即可以得到PQ的解析式,含有m,n的方程,解得Q的坐标值。(2)问,做辅助线,过点D做DM//X轴,交抛物线与M,过点A做AH⊥Y轴,得到矩形,由此证得△ABF≌△AHM,及△AFD≌△AMD,得,∠DFA=∠AFB由于C为中点,∴DG=CB=HD=t,设DF=x,∴DF2=DG2+GF2∴(t+x)2=t2+(2t-x)2 解得x = tan∠DFA=
tan∠DFA= =3. 解:(1)①∵直线BE与
=3. 解:(1)①∵直线BE与 轴平行,点F的坐标为(
轴平行,点F的坐标为(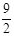 ,1),
,1),∴点B的坐标为(
 ,0),∠FBA=90,BF=1.
,0),∠FBA=90,BF=1.在Rt△EFM中,AF=
 ,
,∴
 .
. ∴点A的坐标为(
 ,0).
,0).∴抛物线的解析式为
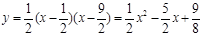 . ......................... 1分
. ......................... 1分②点Q的坐标为
 (
( ,3),
,3), (
( ,5),
,5), (
( ,7). ................... 4分
,7). ................... 4分阅卷说明:答对1个得1分.
(2)∵
 ,
, ,
,∴
 .
.∴
 .
.由
 ,
, .
.解得
 ,
, .
.∵
 ,
,∴点A的坐标为(2,0),点B的坐标为(
 ,0).
,0).∴AB=
 ,即
,即  . ............................................. 5分
. ............................................. 5分方法一:过点D作DG∥
 轴交BE于点G,
轴交BE于点G,AH∥BE交直线DG于点H,延长
DH至点M,使HM=BF.(如图)
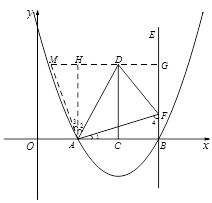
∵DG∥
 轴,AH∥BE,
轴,AH∥BE,∴四边形ABGH是平行四边形.
∵∠ABF=90,
∴四边形ABGH是矩形.
同理四边形CBGD是矩形.
∴AH=GB=CD=AB=GH=
 .
.∵∠HAB=90,∠DAF=45,
∴∠1+∠2=45.
在△AFB和△AMH中,

∴△AFB≌△AMH. 6分
∴∠1=∠3,AF=AM,∠4=∠M.
∴∠3+∠2="45."
在△AFD和△AMD中,

∴△AFD≌△AMD.
∴∠DFA=∠M,FD=MD.
∴∠DFA=∠4. ............................................................ 7分
∵C是AB的中点,
∴DG=CB=HD=
 .
.设BF=
 ,则GF=
,则GF= ,FD=MD=
,FD=MD=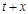 .
.在Rt△DGF中,
 ,
,∴
 ,
,解得
 .
.∴
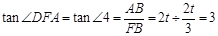 . ...................................... 8分
. ...................................... 8分方法二:过点D作DM⊥AF于M.(如图)

∵CD⊥AB,DM⊥AF,
∴∠NCA=∠DMN=90.
∵∠1=∠2,
∴∠NAC=∠NDM.
∴tan∠NAC=tan∠NDM.
∴
 . …………………………….6分
. …………………………….6分∵C是AB的中点,CD=AB=
 ,
,∴AC=
 ,
, .
.∵∠DAM=45,
∴
 .
. 设 CN=
 ,则DN=
,则DN= .
.∴
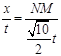 .
.∴
 .
.在Rt△DNM中,
 ,
,∴
 .
. .
. .
.∴
 ,
, (舍).
(舍). ∴CN=
 , ................................................................ 7分
, ................................................................ 7分AN=
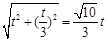 .
.∵EB∥
 轴,
轴,∴EB⊥
 轴.
轴.∵CD⊥AB,
∴CD∥EB.
∴
 .
.∴AF=
 .
.∴MF= AF
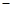 AM=
AM= .
.∴
 . ...................................... 8分
. ...................................... 8分∴考点:
点评:熟练掌握二次函数的性质,三角形的判定,还有正切值的求法,本题的关键是做辅助线的基础上找到等角的关系,由全等三角形的判定知边度关系,再由正切定理把设的未知数舍去而求之,本题做法不唯一,可根据已知灵活应用。属于难题,综合性强,中考易出的题型。

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 的图象如图所示,若
的图象如图所示,若 有两个不相等的实数根,则k的取值范围是 .
有两个不相等的实数根,则k的取值范围是 .
 在
在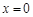 和
和 时的函数值相等。
时的函数值相等。
 的图象与二次函数的图象都经过点
的图象与二次函数的图象都经过点 ,求
,求 和
和 的值;
的值; 轴交于点
轴交于点 (点
(点 在点
在点 的左侧),将二次函数的图象在点
的左侧),将二次函数的图象在点 个单位后得到的图象记为
个单位后得到的图象记为 ,同时将(2)中得到的直线
,同时将(2)中得到的直线 个单位。请结合图象回答:当平移后的直线与图象
个单位。请结合图象回答:当平移后的直线与图象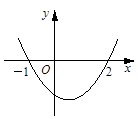
 ,当
,当 时,对应的函数值为y1,当
时,对应的函数值为y1,当 时对应的函数值为
时对应的函数值为 ,若
,若 且
且 时,则( )
时,则( )


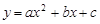 的图象与x轴交于(
的图象与x轴交于(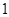 ,0)和(
,0)和(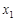 ,0),其中
,0),其中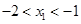 ,与
,与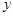 轴交于正半轴上一点.下列结论:①
轴交于正半轴上一点.下列结论:①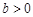 ;②
;②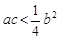 ;③
;③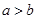 ;④
;④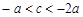 .其中所有正确结论的序号是_______.
.其中所有正确结论的序号是_______. 交y轴于点A,交x轴于点B,C(点B在点C的右侧)。如图,过点A作垂直于y轴的直线l. 在y轴右侧、位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q,交x轴于R,连接AP.
交y轴于点A,交x轴于点B,C(点B在点C的右侧)。如图,过点A作垂直于y轴的直线l. 在y轴右侧、位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q,交x轴于R,连接AP.