题目内容
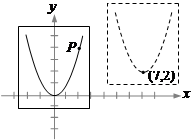
已知抛物线 交y轴于点A,交x轴于点B,C(点B在点C的右侧)。如图,过点A作垂直于y轴的直线l. 在y轴右侧、位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q,交x轴于R,连接AP.
交y轴于点A,交x轴于点B,C(点B在点C的右侧)。如图,过点A作垂直于y轴的直线l. 在y轴右侧、位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q,交x轴于R,连接AP.

(1)求A,B,C三点的坐标;
(2)如果以A,P,Q三点构成的三角形与△AOC相似,求出点P的坐标;
(3)若将△APQ沿AP对折,点Q的对应点为点M. 是否存在点P,使得点M落在x轴上.若存在,求出点P的坐标;若不存在,请说明理由.
 交y轴于点A,交x轴于点B,C(点B在点C的右侧)。如图,过点A作垂直于y轴的直线l. 在y轴右侧、位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q,交x轴于R,连接AP.
交y轴于点A,交x轴于点B,C(点B在点C的右侧)。如图,过点A作垂直于y轴的直线l. 在y轴右侧、位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q,交x轴于R,连接AP.
(1)求A,B,C三点的坐标;
(2)如果以A,P,Q三点构成的三角形与△AOC相似,求出点P的坐标;
(3)若将△APQ沿AP对折,点Q的对应点为点M. 是否存在点P,使得点M落在x轴上.若存在,求出点P的坐标;若不存在,请说明理由.
(1)A(0,4),B(4,0),C(-1,0);(2)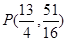 ,
,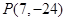 ;(3)
;(3)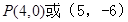
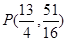 ,
,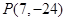 ;(3)
;(3)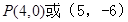
试题分析:(1)分别求得抛物线
 与坐标轴的交点坐标即可得到结果;
与坐标轴的交点坐标即可得到结果;(2)设
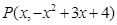 ,则
,则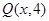 ,
, ,分
,分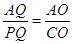 与
与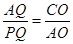 两种情况分析即可得到结果;
两种情况分析即可得到结果;(3)构造正方形PQEF,ME=OA=4,AM=AQ=x,则PM=
 ,证得
,证得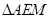 ~
~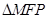 ,根据相似三角形的性质可表示出PF,从而可以表示出CM,在
,根据相似三角形的性质可表示出PF,从而可以表示出CM,在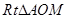 中,根据勾股定理即可列方程求得结果.
中,根据勾股定理即可列方程求得结果.(1)在
 中,
中,当
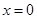 时,
时,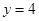 ;
;当
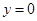 时,
时,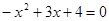 ,解得
,解得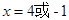
∴A(0,4),B(4,0),C(-1,0);
(2)设
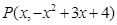 ,则
,则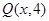 ,
,
当
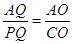 时,得
时,得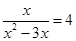 ,解得
,解得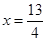
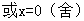 ,此时
,此时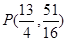
当
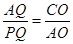 时,得
时,得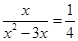 ,解得
,解得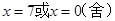 ,此时
,此时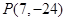 ;
;(3)如图构造正方形PQEF,ME=OA=4,AM=AQ=x
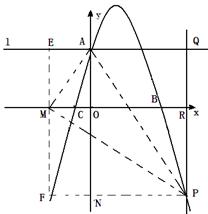
PM=
 ,
,证得
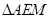 ~
~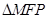
有
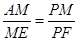 ,即
,即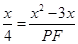 ,解得
,解得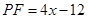
∴
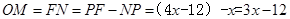
在
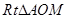 中,
中,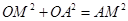
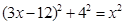
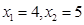
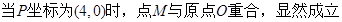
∴
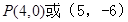 .
.点评:本题知识点多,综合性强,难度较大,一般是中考压轴题,主要考查学生对二次函数的熟练掌握情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
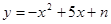 经过点A(1,0),与y轴交于点B。
经过点A(1,0),与y轴交于点B。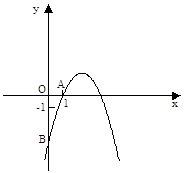
 的图象与x 轴交于(2,0)、(4,0),顶点到x 轴的距离为3,求函数的解析式。
的图象与x 轴交于(2,0)、(4,0),顶点到x 轴的距离为3,求函数的解析式。 与
与 轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与
轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与 轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
 ,
, ),AF=
),AF= .
. ,
, ,且AB的长为
,且AB的长为 ,其中
,其中 .如图2,当∠DAF=45时,求
.如图2,当∠DAF=45时,求 的值和∠DFA的正切值.
的值和∠DFA的正切值.


 AB时,求点E的坐标;
AB时,求点E的坐标; 的最小值是
的最小值是
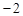
 化成
化成 的形式,则
的形式,则 = .
= .