题目内容
1.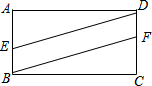 如图,在矩形ABCD中,点E、F分别在AB、DC上,BF∥DE,若AD=12cm,AB=5cm,且AE:EB=3:2,则四边形EBFD的面积为24cm2.
如图,在矩形ABCD中,点E、F分别在AB、DC上,BF∥DE,若AD=12cm,AB=5cm,且AE:EB=3:2,则四边形EBFD的面积为24cm2.
分析 由矩形的性质得出BC=AD=12m,CD=AB=5cm,∠A=∠C=90°,AB∥CD,再证明四边形EBFD是平行四边形,得出BE=DF=2cm,得出AE=CF=3cm,四边形EBFD的面积=矩形ABCD的面积-△ADE的面积-△BCF的面积,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴BC=AD=12m,CD=AB=5cm,∠A=∠C=90°,AB∥CD,
∵AE:EB=3:2,
∴AE=3cm,BE=2cm,
∵BF∥DE,
∴四边形EBFD是平行四边形,
∴BE=DF=2cm,
∴AE=CF=3cm,
∴四边形EBFD的面积=矩形ABCD的面积-△ADE的面积-△BCF的面积
=12×5-$\frac{1}{2}$×12×3-$\frac{1}{2}$×12×3=24(cm2);
故答案为:24cm2.
点评 本题考查了矩形的性质、平行四边形的判定与性质、三角形和四边形面积的计算;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列图案中,既是轴对称又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16. 如图,△ABC与△AED是全等三角形,即△ABC≌△AED,那么图中相等的角有( )
如图,△ABC与△AED是全等三角形,即△ABC≌△AED,那么图中相等的角有( )
 如图,△ABC与△AED是全等三角形,即△ABC≌△AED,那么图中相等的角有( )
如图,△ABC与△AED是全等三角形,即△ABC≌△AED,那么图中相等的角有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
6.一次函数y=(2m+2)x+10中,y随x增大而减小,则( )
| A. | m<-1 | B. | m>-1 | C. | m=1 | D. | m<0 |