题目内容
11.数轴上1,$\sqrt{2}$,对应的点分别记为A,B,且点A为线段BC的中点,设点C表示的数为x,则x+$\sqrt{98}$=2+6$\sqrt{2}$.分析 根据数轴上表示x1和x2的两个点之间的线段的中点,对应的数是$\frac{{x}_{1}+{x}_{2}}{2}$,据此即可求解.
解答 解:根据题意得:$\frac{x+\sqrt{2}}{2}$=1,
解得:x=2-$\sqrt{2}$,
则x+$\sqrt{98}$=2-$\sqrt{2}+7\sqrt{2}$=2$+6\sqrt{2}$,
故答案为:2+6$\sqrt{2}$.
点评 本题考查了实数与数轴,数轴上线段中点的坐标,理解公式是关键.

练习册系列答案
相关题目
6. 如图在平面直角坐标系中,已知A、B分别是x轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,且AOP的面积为6.若△BOP与△DOP的面积相等,则△BOD的面积为( )
如图在平面直角坐标系中,已知A、B分别是x轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,且AOP的面积为6.若△BOP与△DOP的面积相等,则△BOD的面积为( )
 如图在平面直角坐标系中,已知A、B分别是x轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,且AOP的面积为6.若△BOP与△DOP的面积相等,则△BOD的面积为( )
如图在平面直角坐标系中,已知A、B分别是x轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,且AOP的面积为6.若△BOP与△DOP的面积相等,则△BOD的面积为( )| A. | 9 | B. | 12 | C. | 18 | D. | 24 |
20.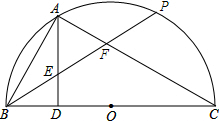 如图所示,已知BC是半圆的直径,P是半圆上一点,过弧BP的中点A作AD⊥BC于点D,BP交AD于点E,交AC于点F,则一定成立的是( )
如图所示,已知BC是半圆的直径,P是半圆上一点,过弧BP的中点A作AD⊥BC于点D,BP交AD于点E,交AC于点F,则一定成立的是( )
 如图所示,已知BC是半圆的直径,P是半圆上一点,过弧BP的中点A作AD⊥BC于点D,BP交AD于点E,交AC于点F,则一定成立的是( )
如图所示,已知BC是半圆的直径,P是半圆上一点,过弧BP的中点A作AD⊥BC于点D,BP交AD于点E,交AC于点F,则一定成立的是( )| A. | AE=EF | B. | AE=AF | C. | AF=EF | D. | AE=EF=AF |
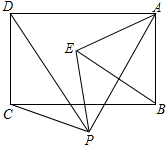 如图,P是矩形ABCD下方一点,将△PCD绕P点顺时针旋转60°后恰好D点与A点重合,得到△PEA,连接EB.
如图,P是矩形ABCD下方一点,将△PCD绕P点顺时针旋转60°后恰好D点与A点重合,得到△PEA,连接EB.