题目内容
17．已知：△ABC∽△DEF的面积之比为1：2，当BC=3时，BC的对应边EF的长是3$\sqrt{2}$．分析 直接根据相似三角形的性质即可得出结论．
解答 解∵△ABC∽△DEF，△ABC与△DEF的面积之比为1：2，
∴$\frac{BC}{EF}$=$\sqrt{\frac{1}{2}}$，
∴EF=3$\sqrt{2}$．
故答案为：3$\sqrt{2}$．
点评 本题考查的是相似三角形的性质，熟知相似三角形面积的比等于相似比的平方是解答此题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
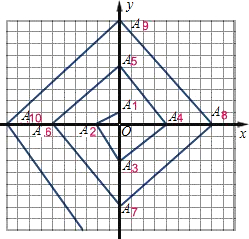如图，在一单位长度为1cm的方格纸上，依如图所示的规律，设定点A1、A2、A3、A4、…An．连接点A1、A2、A3组成三角形，记为△1，面积S1=4；连接A2、A3、A4组成三角形，记为△2，面积S2=9；连接A3、A4、A5组成三角形，记为△3，面积S3=16…，连An、An+1、An+2组成三角形，记为△n（n为正整数），则面积Sn=（n+1）2．
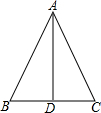如图，在△ABC中，AB=AC，AD是BC边上的中线，则∠BDA=90°．