题目内容
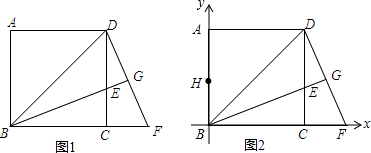
14.已知,如图1,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.(1)求证:△BCE≌△DCF;
(2)求CF的长;
(3)如图2,在AB上取一点H,且BH=CF,若以BC为x轴,AB为y轴建立直角坐标系,问在直线BD上是否存在点P,使得以B、H、P为顶点的三角形为等腰三角形?若存在,直接写出所有符合条件的P点坐标;若不存在,说明理由.
分析 (1)利用正方形的性质,由全等三角形的判定定理SAS即可证得△BCE≌△DCF;
(2)通过△DBG≌△FBG的对应边相等知BD=BF=$\sqrt{2}$;然后由CF=BF-BC=即可求得;
(3)分三种情况分别讨论即可求得.
解答 (1)证明:如图1,
在△BCE和△DCF中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCE=∠DCF=90°}\\{CE=CF}\end{array}\right.$,
∴△BCE≌△DCF(SAS);
(2)证明:如图1,
∵BE平分∠DBC,OD是正方形ABCD的对角线,
∴∠EBC=$\frac{1}{2}$∠DBC=22.5°,
由(1)知△BCE≌△DCF,
∴∠EBC=∠FDC=22.5°(全等三角形的对应角相等);
∴∠BGD=90°(三角形内角和定理),
∴∠BGF=90°;
在△DBG和△FBG中,
$\left\{\begin{array}{l}{∠DBG=∠FBG}\\{BG=BG}\\{∠BGD=∠BGF}\end{array}\right.$,
∴△DBG≌△FBG(ASA),
∴BD=BF,DG=FG(全等三角形的对应边相等),
∵BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{2}$,
∴BF=$\sqrt{2}$,
∴CF=BF-BC=$\sqrt{2}$-1;
(3)解:如图2,∵CF=$\sqrt{2}$-1,BH=CF
∴BH=$\sqrt{2}$-1,
①当BH=BP时,则BP=$\sqrt{2}$-1,
∵∠PBC=45°,
设P(x,x),
∴2x2=($\sqrt{2}$-1)2,
解得x=1-$\frac{\sqrt{2}}{2}$或-1+$\frac{\sqrt{2}}{2}$,
∴P(1-$\frac{\sqrt{2}}{2}$,1-$\frac{\sqrt{2}}{2}$)或(-1+$\frac{\sqrt{2}}{2}$,-1+$\frac{\sqrt{2}}{2}$);
②当BH=HP时,则HP=PB=$\sqrt{2}$-1,
∵∠ABD=45°,
∴△PBH是等腰直角三角形,
∴P($\sqrt{2}$-1,$\sqrt{2}$-1);
③当PH=PB时,∵∠ABD=45°,
∴△PBH是等腰直角三角形,
∴P($\frac{\sqrt{2}-1}{2}$,$\frac{\sqrt{2}-1}{2}$),
综上,在直线BD上是否存在点P,使得以B、H、P为顶点的三角形为等腰三角形,所有符合条件的P点坐标为(1-$\frac{\sqrt{2}}{2}$,1-$\frac{\sqrt{2}}{2}$)、(-1+$\frac{\sqrt{2}}{2}$,-1+$\frac{\sqrt{2}}{2}$)、($\sqrt{2}$-1,$\sqrt{2}$-1)、($\frac{\sqrt{2}-1}{2}$,$\frac{\sqrt{2}-1}{2}$).
点评 本题是四边形的综合题,考查了正方形的性质,三角形全等的判定和性质,等腰三角形的判定,熟练掌握性质定理是解题的关键.

①[0)=0;
②[x)-x的最小值是0;
③[x)-x的最大值是1;
④存在实数x,使[x)-x=0.5成立;
⑤如[x)+x=a,则不大于a的最大整数一定是奇数
其中正确的是( )
| A. | ①③④ | B. | ②③④ | C. | ③④ | D. | ③④⑤ |
| A. | 4 | B. | 4或-4 | C. | 0 | D. | 4或0 |
