题目内容
如图,直线EF∥GH,点B、A分别在直线EF、GH上,连接AB,在AB左侧作三角形ABC,其中∠ACB=90°,且∠DAB=∠BAC,直线BD平分∠FBC交直线GH于D.
(1)若点C恰在EF上,如图1,则∠DBA= .
(2)将A点向左移动,其它条件不变,如图2,则(1)中的结论还成立吗?若成立,证明你的结论;若不成立,说明你的理由.
(3)若将题目条件“∠ACB=90°”,改为:“∠ACB=120°”,其它条件不变,那么∠DBA= .(直接写出结果,不必证明)
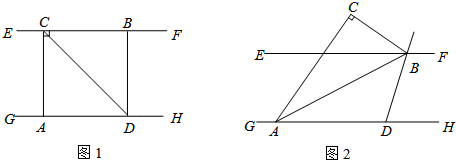
(1)若点C恰在EF上,如图1,则∠DBA=
(2)将A点向左移动,其它条件不变,如图2,则(1)中的结论还成立吗?若成立,证明你的结论;若不成立,说明你的理由.
(3)若将题目条件“∠ACB=90°”,改为:“∠ACB=120°”,其它条件不变,那么∠DBA=
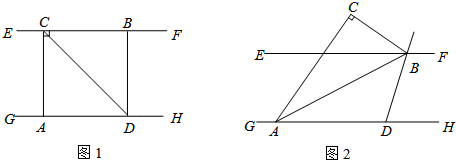
考点:平行线的判定与性质
专题:
分析:(1)根据两直线平行,同旁内角互补求出∠CAD=90°,然后求出∠BAC=45°,从而得到∠ABC=45°,再根据BD平分∠FBC求出∠DBC=90°,然后求解即可;
(2)根据两直线平行,内错角相等可得∠2=∠3,再根据三角形的内角和定理表示出∠4,然后表示∠5,再利用平角等于180°列式表示出∠DBA整理即可得解;
(3)根据(2)的结论计算即可得解.
(2)根据两直线平行,内错角相等可得∠2=∠3,再根据三角形的内角和定理表示出∠4,然后表示∠5,再利用平角等于180°列式表示出∠DBA整理即可得解;
(3)根据(2)的结论计算即可得解.
解答:解: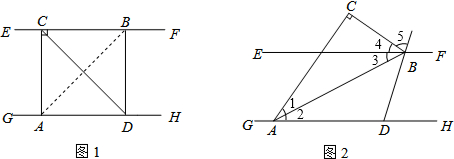 (1)∵EF∥GH,
(1)∵EF∥GH,
∴∠CAD=180°-∠ACB=180°-90°=90°,
∵∠DAB=∠BAC,
∴∠BAC=45°,
∴∠ABC=45°,
∵BD平分∠FBC,
∴∠DBC=
×180°=90°,
∴∠DBA=90°-45°=45°;
(2)解:如图,设∠DAB=∠BAC=x,即∠1=∠2=x,
∵EF∥GH,
∴∠2=∠3,
在△ABC内,∠4=180°-∠ACB-∠1-∠3=180°-∠ACB-2x,
∵直线BD平分∠FBC,
∴∠5=
(180°-∠4)=
(180°-180°+∠ACB+2x)=
∠ACB+x,
∴∠DBA=180°-∠3-∠4-∠5,
=180°-x-(180°-∠ACB-2x)-(
∠ACB+x),
=180°-x-180°+∠ACB+2x-
∠ACB-x,
=
∠ACB,
=
×90°,
=45°;
(3)由(2)可知,∠ACB=120°时,
∠DBA=
×120°=60°.
故答案为:(1)45°,(3)60°.
 (1)∵EF∥GH,
(1)∵EF∥GH,∴∠CAD=180°-∠ACB=180°-90°=90°,
∵∠DAB=∠BAC,
∴∠BAC=45°,
∴∠ABC=45°,
∵BD平分∠FBC,
∴∠DBC=
| 1 |
| 2 |
∴∠DBA=90°-45°=45°;
(2)解:如图,设∠DAB=∠BAC=x,即∠1=∠2=x,
∵EF∥GH,
∴∠2=∠3,
在△ABC内,∠4=180°-∠ACB-∠1-∠3=180°-∠ACB-2x,
∵直线BD平分∠FBC,
∴∠5=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DBA=180°-∠3-∠4-∠5,
=180°-x-(180°-∠ACB-2x)-(
| 1 |
| 2 |
=180°-x-180°+∠ACB+2x-
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=45°;
(3)由(2)可知,∠ACB=120°时,
∠DBA=
| 1 |
| 2 |
故答案为:(1)45°,(3)60°.
点评:本题考查了平行线的性质,角平分线的定义,三角形的内角和定理,熟记性质并理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
下列实数比较大小正确的是( )
A、-
| ||||
B、|-
| ||||
C、3
| ||||
D、2-
|
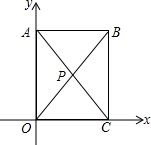 如图,长方形ABCO对角线BO与AC的交点P到相对两边距离相等.若C点(2,0),P(1,2),请写出A,B坐标,你发现A,P,C三点横坐标有什么关系呢?纵坐标呢?
如图,长方形ABCO对角线BO与AC的交点P到相对两边距离相等.若C点(2,0),P(1,2),请写出A,B坐标,你发现A,P,C三点横坐标有什么关系呢?纵坐标呢? 如图,AD平分∠EAC,AD∥BC,试探索∠B与∠C的数量关系,写出你的结论并说明理由.
如图,AD平分∠EAC,AD∥BC,试探索∠B与∠C的数量关系,写出你的结论并说明理由. 如图,△ABC中,AB=AC,∠A=50°,DE是腰AB的垂直平分线,求∠DBC的度数.
如图,△ABC中,AB=AC,∠A=50°,DE是腰AB的垂直平分线,求∠DBC的度数.