��Ŀ����
��ͼ����֪������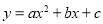 ��x���һ������ΪA��-1��0������һ������ΪB����y��Ľ���ΪC��0��-3�����䶥��ΪD���Գ���Ϊֱ��
��x���һ������ΪA��-1��0������һ������ΪB����y��Ľ���ΪC��0��-3�����䶥��ΪD���Գ���Ϊֱ��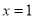 ��
��
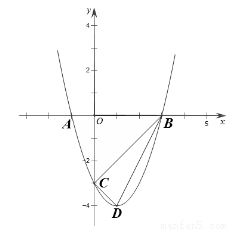
��1���������ߵĽ���ʽ��
��2����֪��MΪy���ϵ�һ�����㣬����ACM����ACΪһ���ĵ���������ʱ�����M�����ꣻ
��3������OBC��x������ƽ��m����λ���ȣ�0��m��3���õ���һ�������Ρ�EFG������EFG���BCD�ص����ֵ������ΪS���ú�m�Ĵ���ʽ��ʾS��
��1�� ����2��M������Ϊ
����2��M������Ϊ ��
�� ��
�� ����3��
����3�� ��
��
��������
�����������1����������x���һ������ΪA��-1��0�����Գ���Ϊֱ�� ���õ���������x�����һ������ΪB��3��0������A��B��C��������������ߣ����ɵõ������ߵĽ���ʽ��
���õ���������x�����һ������ΪB��3��0������A��B��C��������������ߣ����ɵõ������ߵĽ���ʽ��
��2���ٵ�AC=AMʱC��M����x��Գƣ��õ�M ��
��
�ڵ�AC=CMʱ��AC= ����CΪԲ�ģ�ACΪ�뾶��Բ��y�����������㣬ΪM
����CΪԲ�ģ�ACΪ�뾶��Բ��y�����������㣬ΪM ��M
��M ��
��
��3���ֱ����ֱ��BC��BD�Ľ���ʽ�������μ����ص���������� ����
���� ��
��
�����������1���������֪�������� ��x�����һ������ΪB��3��0����
��x�����һ������ΪB��3��0����
�� �����
����� ���������ߵĽ���ʽΪ��
���������ߵĽ���ʽΪ�� ��
��
��2���ٵ�AC=AMʱC��M����x��Գƣ��õ�M ��
��
�ڵ�AC=CMʱ��AC= ����CΪԲ�ģ�ACΪ�뾶��Բ��y�����������㣬ΪM
����CΪԲ�ģ�ACΪ�뾶��Բ��y�����������㣬ΪM ��M
��M ��
��
���ԣ���M������Ϊ ��
�� ��
�� ��
��
��3����ƽ�ƺ��������Ϊ��EFG����ֱ��BC�Ľ���ʽΪy=kx+b���� ����ã�
����ã� ����ֱ��BC�Ľ���ʽΪ
����ֱ��BC�Ľ���ʽΪ ����OBC��x������ƽ��m����λ���ȣ�0��m��3���õ���EFG����ֱ��FG�Ľ���ʽΪ
����OBC��x������ƽ��m����λ���ȣ�0��m��3���õ���EFG����ֱ��FG�Ľ���ʽΪ ����ֱ��BD�Ľ���ʽΪy=k��x+b�䣬��
����ֱ��BD�Ľ���ʽΪy=k��x+b�䣬�� �����
����� ��
��
��ֱ��BD�Ľ���ʽΪ ������CG��ֱ��CG��BD��H����H��
������CG��ֱ��CG��BD��H����H�� ��-3����
��-3����

�ڡ�OBC��x������ƽ�ƵĹ����У�
�ٵ� ʱ����ͼ1��ʾ��
ʱ����ͼ1��ʾ��
��EG��BC�ڵ�P��GF��BD�ڵ�Q����CG=BF=m��BE=PE=3��m������ �����
����� ������Q��3��m��-2m����
������Q��3��m��-2m����
 =
= =
=
�ڵ� ʱ����ͼ2��ʾ��
ʱ����ͼ2��ʾ��

��EG��BC�ڵ�P����BD�ڵ�N����OE=m��BE=PE=3��m������Ϊֱ��BD�Ľ���ʽΪ �����Ե�x=mʱ����y=2m��6�����Ե�N��m��2m-6����
�����Ե�x=mʱ����y=2m��6�����Ե�N��m��2m-6����
 =
= =
= =
= ��
��
���������� ��
��
���㣺���κ����ۺ��⣮



 B��
B�� C��
C�� D��
D��
 ��λ����ͼ��ʾ����tanB��ֵΪ__________��
��λ����ͼ��ʾ����tanB��ֵΪ__________��

 B��
B��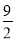 C��
C��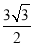 D��
D��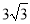
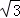 ��1��732��
��1��732��
 ��
�� �Ķ�������Ϊ��0,2��������ABCD�Ķ���B��C��x���ϣ�����ABCD����������x����Χ�ɵ�ͼ����.
�Ķ�������Ϊ��0,2��������ABCD�Ķ���B��C��x���ϣ�����ABCD����������x����Χ�ɵ�ͼ����.

 B��
B�� C��
C�� D��1
D��1