题目内容
已知:如图,二次函数 的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,矩形ABCD在抛物线与x轴所围成的图形内.
的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,矩形ABCD在抛物线与x轴所围成的图形内.

(1)求二次函数的表达式;
(2)设点A的坐标为(x,y)(x>0,y>0),试求矩形ABCD的周长P关于自变量x的函数表达式,并求出自变量x的取值范围.
(1) (2)P=2(
(2)P=2( )+
)+ ,0<x<2
,0<x<2
【解析】
试题分析:(1)直接把顶点坐标代入函数的解析式即可求得m的值,从而得到函数的解析式;
(2)由A点在函数的图像上,可设坐标为(x, ),根据矩形的周长公式可求P关于x的函数关系式,然后令y=0,则有
),根据矩形的周长公式可求P关于x的函数关系式,然后令y=0,则有 =0,因此可求x=±2,得到二次函数与x轴的交点,从而判断出x的取值范围.
=0,因此可求x=±2,得到二次函数与x轴的交点,从而判断出x的取值范围.
试题解析:【解析】
(1)∵
∴抛物线的顶点坐标为(0,4m).
∴4m=2,即 .
.
∴二次函数的表达式为
∵点A在抛物线上,
∴ .
.
∴矩形ABCD的周长P=2( )+
)+ .
.
令y=0,则 =0,
=0,
∴ .
.
∴抛物线与x轴的两个交点是(-2,0),(2,0)
∴关于x的函数P的自变量的取值范围0<x<2.
考点:二次函数的图像与性质,矩形的周长

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 平移后经过点
平移后经过点 ,
, ,求平移后的抛物线的表达式.
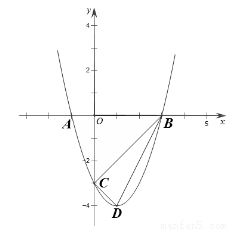
,求平移后的抛物线的表达式.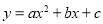 与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C(0,-3),其顶点为D,对称轴为直线
与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C(0,-3),其顶点为D,对称轴为直线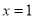 .
.

 B.
B. C.
C. D.
D.
 ,则锐角A的度数是( )
,则锐角A的度数是( ) B.
B. C.
C. D.
D.


 ,那么∠A等于( )
,那么∠A等于( )