题目内容
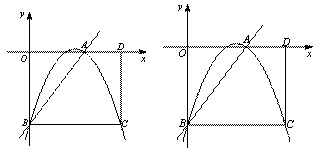
如图,矩形OBCD的边OD、OB分别在x轴正半轴和y轴负半轴上,且OD=10,
OB=8.将矩形的边BC绕点B逆时针旋转,使点C恰好与x轴上的点A重合.
(1)若抛物线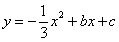 经过A、B两点,求该抛物线的解析式:______________;
经过A、B两点,求该抛物线的解析式:______________;
(2)若点M是直线AB上方抛物线上的一个动点,
作MN⊥x轴于点N.是否存在点M,使△AMN
与△ACD相似?若存在,求出点M的坐标;
若不存在,说明理由.
 |
解:(1)∵AB=BC=10,OB=8 ∴在Rt△OAB中,OA=6 ∴ A(6,0)
将A(6,0),B(0,-8)代入抛物线表达式,得,
 (2)存在:
(2)存在:
如果△AMN与△ACD相似,则 或
或
设M (0<m<6)
(0<m<6)
1) 假设点M在x轴下方的抛物线上,如图1所示:
当 时,
时, ,
,
 即
即 ∴
∴ ∴
∴
如图2验证一下:当 时,
时, ,即
,即
∴ (舍)
(舍)
2)如果点M在x轴上方的抛物线上:当 时,
时, ,即
,即 ∴
∴ ∴M
∴M
此时 ,
, ∴
∴ ∴△AMN∽△ACD ∴M
∴△AMN∽△ACD ∴M 满足要求
满足要求
当 时,
时, ,即
,即 ∴m=10(舍)
∴m=10(舍)
综上M1 ,M2
,M2

练习册系列答案
相关题目
 这两次拐弯的角度可能是( )
这两次拐弯的角度可能是( )
 △AOB绕点O逆时针旋转90°后得到△
△AOB绕点O逆时针旋转90°后得到△ .
.
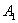 ,
,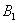 的坐标;
的坐标;
 与抛物线
与抛物线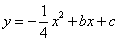 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8. 
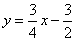 与
与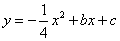 交于A,B两点,点A在x轴上,点B的横坐标为-8.
交于A,B两点,点A在x轴上,点B的横坐标为-8.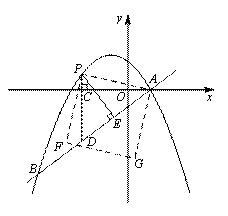
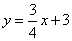 与直线BC:
与直线BC: 相交于点C,分别交x轴于点A、B,P为x轴上的一点,设P(m,0),以点P为圆心作圆:
相交于点C,分别交x轴于点A、B,P为x轴上的一点,设P(m,0),以点P为圆心作圆: 的倒数是 ,写出一个比-3大而比-2小的无理数是 .
的倒数是 ,写出一个比-3大而比-2小的无理数是 .