题目内容
如图,在平面直角坐标系中,直线 与抛物线
与抛物线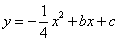 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.设△PDE的周长为l,
点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值.
 |
解:(1)对于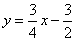 ,当y=0,x=2;当x=
,当y=0,x=2;当x= 8时,y=
8时,y=
 .
.
 ∴A点坐标为(2,0),B点坐标为
∴A点坐标为(2,0),B点坐标为
由抛物线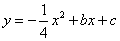 经过A、B两点,得
经过A、B两点,得
 解得
解得

(2)设直线 与y轴交于点M
与y轴交于点M
当x=0时,y= . ∴OM=
. ∴OM=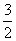 .
.
∵点A的坐标为(2,0),∴OA=2,∴AM=
∴OM:OA:AM=3:4:5.
由题意得,∠PDE=∠OMA,∠AOM=∠PED=90°,∴△AOM ∽△PED.
∴DE:PE:PD=3:4:5
∵点P是直线AB上方的抛物线上一动点,
∴PD =
=
∴


由题意知:


练习册系列答案
相关题目



 cm C.
cm C. cm D.
cm D. cm
cm , CD=
, CD=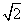 ,高CE=
,高CE=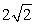 ,对角线AC、BD交于点H.平行于线段BD的两条直线MN、RQ同时从点A出发,沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G,当直线RQ到达点C时,两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的面积为
,对角线AC、BD交于点H.平行于线段BD的两条直线MN、RQ同时从点A出发,沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G,当直线RQ到达点C时,两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的面积为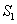 ,被直线RQ扫过的面积为
,被直线RQ扫过的面积为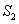 ,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒.
,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒.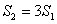 ,求x.
,求x.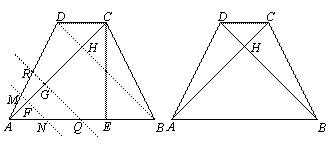
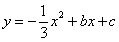 经过A、B两点,求该抛物线的解析式:______________;
经过A、B两点,求该抛物线的解析式:______________;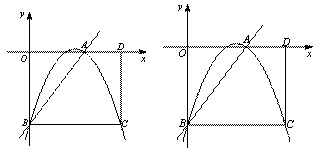
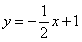 与坐标轴交于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线的另一个交点为E.
与坐标轴交于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线的另一个交点为E.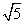 个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止,设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止,设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;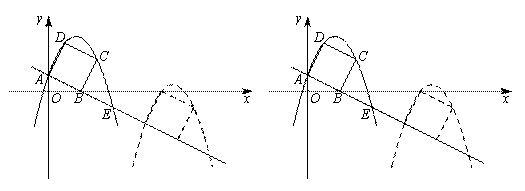
 (B)
(B) (C)
(C) (D)
(D)



 ,则AB=_______;(2)若以AD为直径的⊙O恰与BC边相切,⊙O交AB于E,交AC于F. 过O点的直线MN分别交线段BE和CF于M,N,且AM:MB=3:5,则AN:NC的值为______________.
,则AB=_______;(2)若以AD为直径的⊙O恰与BC边相切,⊙O交AB于E,交AC于F. 过O点的直线MN分别交线段BE和CF于M,N,且AM:MB=3:5,则AN:NC的值为______________. 