题目内容
3.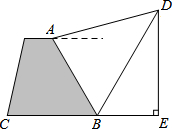 如图,小明站在看台上的A处,测得旗杆顶端D的仰角为15°,当旗杆顶端D的影子刚好落在看台底部B处时,太阳光与地面成60°角.已知∠ABC=60°,AB=4米,求旗杆的高度.(点A与旗杆DE及其影子在同一平面内,C、B、E三点共线且旗杆与地面垂直,不考虑小明的身高)
如图,小明站在看台上的A处,测得旗杆顶端D的仰角为15°,当旗杆顶端D的影子刚好落在看台底部B处时,太阳光与地面成60°角.已知∠ABC=60°,AB=4米,求旗杆的高度.(点A与旗杆DE及其影子在同一平面内,C、B、E三点共线且旗杆与地面垂直,不考虑小明的身高)
分析 利用题中所给的角的度数可得到△ABD中各角的度数,进而把已知线段AB整理到直角三角形中,利用相应的三角函数即可求得所求线段的长度.
解答  解:过点A作AF⊥BD于点F,
解:过点A作AF⊥BD于点F,
由题意知,∠DAH=15°,∠DBE=60°,
C、B、E三点共线,
∴∠ABD=180°-∠ABC-∠DBE=60°,
在△ABF中,∠AFB=90°,AB=4,
∴BF=AB•cos∠ABD=4×cos60°=2,AF=AB•sin∠ABD=4×sin60°=2$\sqrt{3}$,
∵AH∥CE,
∴∠HAB=∠ABC=60°,
∴∠BAD=∠HAB+∠DAH=75°,
在△DAB中,∠ADB=180°-∠ABD-∠DAB=45°,
∴在RT△ADF中,DF=AF•tan∠ADB=2$\sqrt{3}$,
∴BD=BF+FD=2+2$\sqrt{3}$,
在RT△BDE中,∠DBE=60°
∴DE=BD•sin∠DBE=(2+2$\sqrt{3}$)×$\frac{\sqrt{3}}{2}$=3+$\sqrt{3}$,
∴旗杆的高度为(3+$\sqrt{3}$米.
点评 本题考查了解直角三角形-仰角的问题,解题的一般思路是通常把已知长度的线段整理到直角三角形中,利用公共边及相应的三角函数求解;所求的线段的长度也要进行代换,整理到相应的直角三角形中.

练习册系列答案
相关题目
10.下列图形是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 重合,折痕为EF.若AB=3cm,BC=5cm.
重合,折痕为EF.若AB=3cm,BC=5cm.
 ;
;  ;
; ;
; .
. 如图,△ABC与△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,请找出一条与线段CE相等的线段(以图中已知点的端点),画出这条线段并给出证明.
如图,△ABC与△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,请找出一条与线段CE相等的线段(以图中已知点的端点),画出这条线段并给出证明.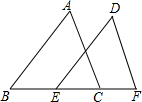 如图,已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,若要以“SAS”为依据,还缺条件AB=DE;若要以“ASA”为依据,还缺条件∠ACB=∠DFE,若要以“AAS”为依据,还缺条件∠A=∠D.
如图,已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,若要以“SAS”为依据,还缺条件AB=DE;若要以“ASA”为依据,还缺条件∠ACB=∠DFE,若要以“AAS”为依据,还缺条件∠A=∠D.