题目内容
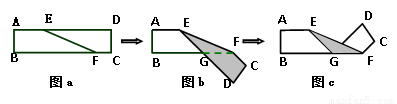
17. 如图,已知△ABC中,AB>AC,BC=6,BC边上的高AN=4.直角梯形DEFG的底EF在BC边上,EF=4,点D、G分别在边AB、AC上,且DG∥EF,GF⊥EF,垂足为F.设GF的长为x,直角梯形DEFG的面积为y,求y关于x的函数关系式,并写出函数的定义域.
如图,已知△ABC中,AB>AC,BC=6,BC边上的高AN=4.直角梯形DEFG的底EF在BC边上,EF=4,点D、G分别在边AB、AC上,且DG∥EF,GF⊥EF,垂足为F.设GF的长为x,直角梯形DEFG的面积为y,求y关于x的函数关系式,并写出函数的定义域.
分析 由平行线分线段成比例定理得出$\frac{DG}{BC}$=$\frac{AG}{AC}$,证出四边形GFMN为矩形,得出GF=MN=x,由平行线分线段成比例定理得出$\frac{AG}{AC}$=$\frac{AM}{AN}$,得出$\frac{DG}{6}$=$\frac{4-x}{4}$,因此DG=6-$\frac{3}{2}$x,即可得出结果.
解答 解:∵DG∥EF,
∴DG∥BC,
∴$\frac{DG}{BC}$=$\frac{AG}{AC}$,
∵GF⊥EF,AN⊥BC,四边形DEFG为直角梯形,
∴四边形GFMN为矩形,
∴GF=MN=x,
∵DG∥BC,
∴$\frac{AG}{AC}$=$\frac{AM}{AN}$=$\frac{AN-GF}{AN}$=$\frac{4-x}{4}$,
∴$\frac{DG}{BC}$=$\frac{4-x}{4}$,
即:$\frac{DG}{6}$=$\frac{4-x}{4}$,
解得:DG=6-$\frac{3}{2}$x,
∴y=$\frac{(DG+EF)}{2}$•MN=$\frac{(6-\frac{3}{2}x+4)}{2}$•x=-$\frac{3}{4}$x2+5x,
即y关于x的函数关系式为:y═-$\frac{3}{4}$x2+5x(0<x<4).
点评 本题考查了平行线分线段成比例定理、直角梯形面积的计算、矩形的判定与性质;本题难度适中,由平行线分线段成比例定理得出比例式是解决问题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
9.为了打击信息诈骗和反信息骚扰,深圳移动公司从2015年9月到10月间,共拦截疑似诈骗电话呼叫1298万次,1298万用科学记数法可表示为( )
| A. | 1298×104 | B. | 12.98×106 | C. | 1.298×107 | D. | 1.298×103 |
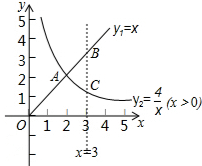 如图所示,函数y1=x(x>0),y2=$\frac{4}{x}$(x>0)的图象交于点A,与直线x=3分别交于B,C两点,给出以下四个结论:
如图所示,函数y1=x(x>0),y2=$\frac{4}{x}$(x>0)的图象交于点A,与直线x=3分别交于B,C两点,给出以下四个结论: 如图,在△ABC中,DE∥BC,当△ADE与△ABC的周长比为1:3时,那么DE:BC=1:3.
如图,在△ABC中,DE∥BC,当△ADE与△ABC的周长比为1:3时,那么DE:BC=1:3.