题目内容
18.如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B、C向过点A的直线作垂线,垂足分别为点E、F.(1)如图(1),过A的直线与斜边BC不相交时,求证:①△ABE≌△CAF; ②EF=BE+CF
(2)如图(2),过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,试求EF的长.
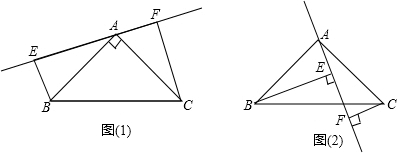
分析 (1)①由条件可求得∠EBA=FAC,利用AAS可证明△ABE≌△CAF;②利用全等三角形的性质可得EA=FC,EB=FA,利用线段的和差可证得结论;
(2)同(1)可证明△ABE≌△CAF,可证得EF=FA-EA,代入可求得EF的长.
解答 (1)证明:
①∵BE⊥EF,CF⊥EF,
∴∠AEB=∠CFA=90°,
∴∠EAB+∠EBA=90°,
∵∠BAC=90°,
∴∠EAB+∠FAC=90°,
∴∠EBA=∠FAC,
在△AEB与△CFA中
$\left\{\begin{array}{l}{∠AEB=∠CFA}\\{∠EBA=∠FAC}\\{AB=CA}\end{array}\right.$
∴△ABE≌△CAF(AAS),
②∵△ABE≌△CAF,
∴EA=FC,EB=FA,
∴EF=AF+AE
=BE+CF;
(2)解:∵BE⊥AF,CF⊥AF
∴∠AEB=∠CFA=90°
∴∠EAB+∠EBA=90°
∵∠BAC=90°
∴∠EAB+∠FAC=90°
∴∠EBA=∠FAC,
在△AEB与△CFA中
$\left\{\begin{array}{l}{∠AEB=∠CFA}\\{∠EBA=∠FAC}\\{AB=CA}\end{array}\right.$
∴△ABE≌△CAF(AAS),
∴EA=FC,EB=FA,
∴EF=FA-EA=EB-FC=10-3=7.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.

练习册系列答案
相关题目
8.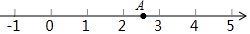 如图所示的数轴上,
如图所示的数轴上,
(1)A点表示数为2.5.
(2)已知点B表示$\frac{7}{4}$,点C表示2$\frac{2}{3}$;在数轴上分别画出点B、C,并将A、B、C所表示的数用“<”连接起来.
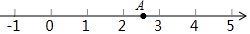 如图所示的数轴上,
如图所示的数轴上,(1)A点表示数为2.5.
(2)已知点B表示$\frac{7}{4}$,点C表示2$\frac{2}{3}$;在数轴上分别画出点B、C,并将A、B、C所表示的数用“<”连接起来.
9.在20人的青年歌手比赛中,规定前10 名晋级,某个选手想知道自己能否晋级,应该选取( )
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
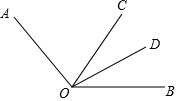 如图,已知∠AOC=80°,∠BOC=50°,OD平分∠BOC,求∠AOD.
如图,已知∠AOC=80°,∠BOC=50°,OD平分∠BOC,求∠AOD.