题目内容
如图,已知二次函数L1: 和二次函数L2:
和二次函数L2: (
( )图象的顶点分别为M,N , 与
)图象的顶点分别为M,N , 与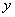 轴分别交于点E, F.
轴分别交于点E, F.
(1) 函数 的最小值为 ;当二次函数L1 ,L2 的
的最小值为 ;当二次函数L1 ,L2 的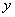 值同时
值同时
随着 的增大而减小时,
的增大而减小时, 的取值范围是 ;
的取值范围是 ;
(2)当 时,求
时,求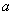 的值,并判断四边形
的值,并判断四边形 的形状(直接写出,不必证明);
的形状(直接写出,不必证明);
(3)若二次函数L2 的图象与 轴的右交点为
轴的右交点为 ,当△
,当△ 为等腰三角形时,求方程
为等腰三角形时,求方程 的解.
的解.

解析:(1)∵ , ∴
, ∴ ;
;
∵ ,∴当
,∴当 时,L1的
时,L1的 值随着
值随着 的增大而减小,当
的增大而减小,当 时, L2 的
时, L2 的 值随着
值随着 的增大而减小, ∴
的增大而减小, ∴ 的取值范围是
的取值范围是
(2)∵ , ∴
, ∴ ,
,
 ∵
∵ ,∴
,∴ ,
,
∴ ,
,
如图,∵ , ∴
, ∴ ,
,
∴ ,∴
,∴
∵ ,∴
,∴
∴ , ∴
, ∴
∴四边形 是平行四边形,
是平行四边形,
已知 ,
,
∴四边形 是矩形(对角线相等且互相平分的四边形是矩形)
是矩形(对角线相等且互相平分的四边形是矩形)
(3)∵ ,
, ,
,
∴
① 当 时,有
时,有 ,∴
,∴ ,等式不成立;
,等式不成立;
② 当 时,有
时,有 ∴
∴ ;
;
③ 当 时,有
时,有 ,∴
,∴
∴ 或
或 , ∵
, ∵ 的对称轴为
的对称轴为 ,
,
∴左交点坐标分别是(-4,0)或( ,0),
,0),
∴方程 的解为
的解为  .
.


在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1) 先从袋子中取出m (m>1)个红球,再从袋子中随机摸出一个球,将“摸出黑球”记为事件A.
请完成下列表格:
| 事件A | 必然事件 | 随机事件 |
| m的值 |
(2) 先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出一个球是黑球的概率等于 ,求m的值.
,求m的值.
 ,则
,则 等于( )
等于( )
 D.-
D.- ,其中
,其中
 的两根为m,n ,则
的两根为m,n ,则 = .
= .
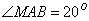 ,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则
,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则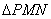 周长的最小值为( )
周长的最小值为( )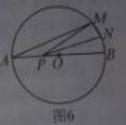

 马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为
马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为 ,B处的俯角为
,B处的俯角为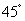 .如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是
.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是 