题目内容
10.计算:(1)$\sqrt{16}$-$\root{3}{125}$+|$\sqrt{3}$-2|
(2)(2$\sqrt{3}$+3$\sqrt{2}$)-|-$\sqrt{2}$|(精确到0.01)
(3)求x的值:3(x+1)2-27=0.
分析 (1)原式利用平方根,立方根以及绝对值的代数意义化简,计算即可得到结果;
(2)原式利用绝对值的代数意义化简,合并后取近似值即可;
(3)原式变形后,利用平方根定义开方即可求出x的值.
解答 解:(1)原式=4-5+2-$\sqrt{3}$=1-$\sqrt{3}$;
(2)原式=2$\sqrt{3}$+3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{3}$+2$\sqrt{2}$≈6.29;
(3)3(x+1)2=27,
变形得:(x+1)2=9,
开方得:(x+1)=3或(x+1)=-3,
解得:x=2或x=-4.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.如果∠A与∠B的两边互相垂直,则∠A与∠B的关系为( )
| A. | ∠A=∠B | B. | ∠A+∠B=90° | ||
| C. | ∠A+∠B=180° | D. | ∠A=∠B或∠A+∠B=180° |
15.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
| A. | AB=CD | B. | AC=BD | C. | AB=BC | D. | AD=BC |
2.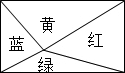 一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是21cm2,则该矩形的面积为( )
一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是21cm2,则该矩形的面积为( )
 一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是21cm2,则该矩形的面积为( )
一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是21cm2,则该矩形的面积为( )| A. | 60cm2 | B. | 70cm2 | C. | 120cm2 | D. | 140cm2 |
19. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )| A. | 44° | B. | 60° | C. | 67° | D. | 70° |
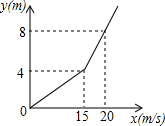 行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑行一段距离才停止,这段距离称为“刹车距离”,为了测定某种型号汽车的刹车性能,对这种汽车进行测试,测得汽车的刹车距离y(m)与车速x(m/s)满足函数关系图象如图所示:
行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑行一段距离才停止,这段距离称为“刹车距离”,为了测定某种型号汽车的刹车性能,对这种汽车进行测试,测得汽车的刹车距离y(m)与车速x(m/s)满足函数关系图象如图所示: