题目内容
10．因式分解：（1）a3-16a
（2）（a2+4）-16a2．
分析 （1）原式提取a，再利用平方差公式分解即可；
（2）原式利用平方差公式及完全平方公式分解即可．
解答 解：（1）原式=a（a2-16）=a（a+4）（a-4）；
（2）原式=（a2+4+4a）（a2+4-4a）=（a+2）2（a-2）2．
点评 此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
中考解读考点精练系列答案
相关题目
1．
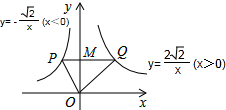函数y=-$\frac{\sqrt{2}}{x}$（x＜0）和y=$\frac{2\sqrt{2}}{x}$（x＞0）的图象如图所示，O为坐标原点，M是y轴正半轴上任意一点，过点M作PQ∥x轴，分别与图中的函数图象相交于P、Q两点，连接OP、OQ，则△OPQ的面积为（ ）
函数y=-$\frac{\sqrt{2}}{x}$（x＜0）和y=$\frac{2\sqrt{2}}{x}$（x＞0）的图象如图所示，O为坐标原点，M是y轴正半轴上任意一点，过点M作PQ∥x轴，分别与图中的函数图象相交于P、Q两点，连接OP、OQ，则△OPQ的面积为（ ）| A． | $\sqrt{2}$ | B． | $\frac{3}{2}\sqrt{2}$ | C． | 2$\sqrt{2}$ | D． | $\frac{5}{2}\sqrt{2}$ |
18．甲、乙两人5次射击命中的环数如下：
则这两人5次射击命中的环数的平均数$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$=8，方差S甲2（ ）S乙2．
| 甲 | 7 | 9 | 8 | 6 | 10 |
| 乙 | 7 | 8 | 9 | 8 | 8 |
| A． | ＞ | B． | ＜ | C． | = | D． | 以上都不对 |