题目内容
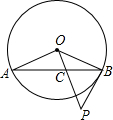 如图,AB为⊙O的弦,PB切⊙O于点B,OP⊥OA,交AB于点C,求证:PB=PC.
如图,AB为⊙O的弦,PB切⊙O于点B,OP⊥OA,交AB于点C,求证:PB=PC.考点:切线的性质
专题:证明题
分析:由切线的性质及OP⊥OA,可得到∠OCA=∠CBP,结合对顶角相等可得到∠PCB=∠PBC,得出结论.
解答:证明:因为PB切圆O于B点,
所以∠PBO=90,
即∠OBA+∠PBA=90,
因为OP⊥OA,
即∠COA=90,
所以∠A+∠ACO=90,
因为OA=OB,
所以∠A=∠OBA,
所以∠ACO=∠PBA,
因为∠ACO=∠PCB,
所以∠PCB=∠PBA,
所以PB=PC.
所以∠PBO=90,
即∠OBA+∠PBA=90,
因为OP⊥OA,
即∠COA=90,
所以∠A+∠ACO=90,
因为OA=OB,
所以∠A=∠OBA,
所以∠ACO=∠PBA,
因为∠ACO=∠PCB,
所以∠PCB=∠PBA,
所以PB=PC.
点评:本题主要考查切线的性质,已知切线和切点连接圆心和切点是解题的常用方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,直线a与直线c相交于点O,则∠1的度数是( )
如图,直线a与直线c相交于点O,则∠1的度数是( )| A、60° | B、50° |
| C、40° | D、30° |
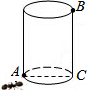 如图,圆柱体蜜桶的半径为1cm,高为3cm,桶内所装蜜的高度距点B为1cm,在点A处有一只蚂蚁,若蚂蚁沿圆柱体的外表面爬行到内表面BC 线的某点处吃蜜,它爬行的最短路线是多少?
如图,圆柱体蜜桶的半径为1cm,高为3cm,桶内所装蜜的高度距点B为1cm,在点A处有一只蚂蚁,若蚂蚁沿圆柱体的外表面爬行到内表面BC 线的某点处吃蜜,它爬行的最短路线是多少? 如图,∠AOB和∠COD都是直角,OE是OD的反向延长线.
如图,∠AOB和∠COD都是直角,OE是OD的反向延长线.