题目内容
4.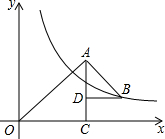 如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为9.
如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为9.
分析 先设点B坐标,再由等腰直角三角形的性质得出OA=$\sqrt{2}$AC,AB=$\sqrt{2}$AD,OC=AC,AD=BD,代入OA2-AB2=18,得到ab=9,即可求得k的值.
解答 解:设点B(a,b),
∵△OAC和△BAD都是等腰直角三角形,
∴OA=$\sqrt{2}$AC,AB=$\sqrt{2}$AD,OC=AC,AD=BD,
∵OA2-AB2=18,
∴2AC2-2AD2=18即AC2-AD2=9
∴(AC+AD)(AC-AD)=9,
∴(OC+BD)•CD=9,
∴ab=9,
∴k=9,
故答案为9.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
9.已知正方形ABCD,点E在线段BC上,且BE=2CE,连接AE,将△ABE沿AE翻折,点B落在点B1处,则tan∠DAB1的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{12}$ |
16.某课外小组的同学们实践活动中调查了20户家庭某月用电量,如表所示:
则这户家庭用电量的众数和中位数分别是( )
| 用电量(度) | 120 | 140 | 160 | 180 | 220 |
| 户数 | 2 | 4 | 5 | 7 | 2 |
| A. | 180,160 | B. | 160,180 | C. | 160,160 | D. | 180,180 |
13.在下面的四个几何体中,主视图是三角形的是( )
| A. | 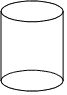 | B. | 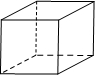 | C. | 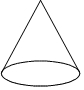 | D. |  |
 如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD=$\frac{3}{4}$.
如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD=$\frac{3}{4}$. 如图,小明于堤边A处垂钓,河堤AB的坡比为1:$\sqrt{3}$,坡长为3米,钓竿AC的倾斜角是60°,其长为6米,若钓竿AC与钓鱼线CD的夹角为60°,求浮漂D与河堤下端B之间的距离.
如图,小明于堤边A处垂钓,河堤AB的坡比为1:$\sqrt{3}$,坡长为3米,钓竿AC的倾斜角是60°,其长为6米,若钓竿AC与钓鱼线CD的夹角为60°,求浮漂D与河堤下端B之间的距离.