题目内容
已知:线段AB=5cm,延长AB到C,使AC=7cm,在AB的反向延长线上取点D,使BD=4BC,设线段CD的中点为E,问线段AE是线段CD的几分之一?
分析:根据题意和图形,即可推出BC的长度,然后根据BD=4BC,即可推出BD的长度,继而即可推出AD=3,由图形可推出CD=BD+BC=10cm,由E点为CD的中点,即可推出DE的长度,由AE=DE-AD=5-3=2cm,由AE和CD的长度即可推出线段AE是线段CD的几分之一.
解答:解:

∵BC=AC-AB,AC=7,AB=5,
∴BC=2,
∴BD=4BC=8,
∴AD=BD-AB=3,
∵CD=BD+BC,
∴CD=10(cm),
∴E为CD的中点,
∴DE=
CD=5,
∴AE=DE-AD=2(cm),
∴AE是CD的
.

∵BC=AC-AB,AC=7,AB=5,
∴BC=2,
∴BD=4BC=8,
∴AD=BD-AB=3,
∵CD=BD+BC,
∴CD=10(cm),
∴E为CD的中点,
∴DE=
| 1 |
| 2 |
∴AE=DE-AD=2(cm),
∴AE是CD的
| 1 |
| 5 |
点评:本题主要考查线段中点的概念,两点之间的距离等知识点,关键在于运用数形结合的思想推出AE和CD的长度,认真的进行计算.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知线段AB等于2个单位长,C是线段AB的黄金分割点,则AC的长度为( )
A、
| ||||
B、3-
| ||||
C、
| ||||
| D、以上结论都不对 |
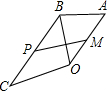 已知:如图,在△AOB中,AB=2,C为平面内一点,且OC=3,线段OC绕点O旋转一周,连接BC,M、P分别为OA、BC的中点,则在OC旋转的过程中PM的范围为( )
已知:如图,在△AOB中,AB=2,C为平面内一点,且OC=3,线段OC绕点O旋转一周,连接BC,M、P分别为OA、BC的中点,则在OC旋转的过程中PM的范围为( )| A、2<PM<3 | B、1<PM≤2.5 | C、0.5≤PM<3 | D、0.5≤PM≤2.5 |
已知:点C在直线AB上,线段AB=6,点D是AC中点,BC=4那么A、D之间的距离是( )
| A、5 | B、2.5 | C、5或1 | D、5或2.5 |
 10、如图已知∠ACB=90°,CD⊥AB于D,则图中表示点到直线的距离的线段的条数是( )
10、如图已知∠ACB=90°,CD⊥AB于D,则图中表示点到直线的距离的线段的条数是( ) 如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知△PAB的周长为14,PA=4,则线段AB的长度为( )
如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知△PAB的周长为14,PA=4,则线段AB的长度为( )