题目内容
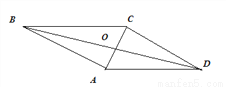
在?ABCD中(非矩形),连接AC,△ABC为直角三角形,若AB=4,AC=3,则AD=________.
【答案】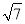 或5
或5
【解析】(1)如图,四边形是平行四边形,利用勾股定理知,CD=AB,AD=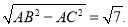
(2) 四边形是平行四边形,利用勾股定理知,BC=AD=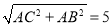 .
.
【题型】填空题
【结束】
20
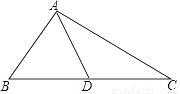
如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=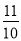 ,则tan∠BAD=________.
,则tan∠BAD=________.
练习册系列答案
相关题目
题目内容
在?ABCD中(非矩形),连接AC,△ABC为直角三角形,若AB=4,AC=3,则AD=________.
【答案】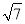 或5
或5
【解析】(1)如图,四边形是平行四边形,利用勾股定理知,CD=AB,AD=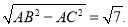

(2) 四边形是平行四边形,利用勾股定理知,BC=AD=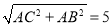 .
.

【题型】填空题
【结束】
20
如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=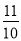 ,则tan∠BAD=________.
,则tan∠BAD=________.
