题目内容
4.把函数y=x2+bx+c的图象向左平移2个单位再向上平移3个单位,所得图象的解析式为y=x2+2x+3,则b、c的值为( )| A. | b=2,c=0 | B. | b=2,c=-2 | C. | b=-2,c=-1 | D. | b=-2,c=0 |
分析 先把得到新的图象的解析式进行变形,再将新抛物线y=(x+1)2+2向下平移3个单位,再向右平移2个单位得到原抛物线的顶点式解析式,再化为一般式即可得出答案.
解答 解:∵所得图象的解析式为y=x2+2x+3,
∴y=(x+1)2+2,
∴将新二次函数y=(x+1)2+2向下平移3个单位,再向右平移2个单位,
得到的解析式为y=(x+1-2)2+2-3,即y=(x-1)2-1,
∴y=x2-2x,
又∵y=x2+bx+c,
∴b=-2,c=0;
故选D.
点评 此题考查了二次函数图象和几何变换,熟练掌握二次函数的平移的规律:左加右减,上加下减是本题的关键,注意要先把新函数图象变成顶点式,再进行求解.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
15.在平面直角坐标系中,已知点A(-1,2),则点A关于x轴的对称点B的坐标是( )
| A. | (-1,-2) | B. | (1,2) | C. | (2,-1) |
19.在-$\frac{1}{3}$,$\frac{1}{2013}$,-1,0这四个数中最小的是( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{2013}$ | C. | -1 | D. | 0 |
9. 如图所示格点图中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABC缩小,则点C的对应点C′的坐标为( )
如图所示格点图中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABC缩小,则点C的对应点C′的坐标为( )
 如图所示格点图中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABC缩小,则点C的对应点C′的坐标为( )
如图所示格点图中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABC缩小,则点C的对应点C′的坐标为( )| A. | (1,$\frac{3}{2}$) | B. | (2,6) | C. | (2,6)或(-2,-6) | D. | (1,$\frac{3}{2}$)或(-1,-$\frac{3}{2}$) |
14.估计$\sqrt{7}$的值介于( )
| A. | 0与1之间 | B. | 1与2之间 | C. | 2与3之间 | D. | 3与4之间 |
 若抛物线y=ax2+bx+c如图所示,下列四个结论:
若抛物线y=ax2+bx+c如图所示,下列四个结论: 已知反比例函数y=$\frac{k}{x}$(k≠0)的图象如图所示,则k的值可能是-1(写一个即可).
已知反比例函数y=$\frac{k}{x}$(k≠0)的图象如图所示,则k的值可能是-1(写一个即可).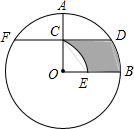 如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=$\sqrt{3}$,以O为圆心,OC为半径作$\widehat{CE}$,交OB于E点.
如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=$\sqrt{3}$,以O为圆心,OC为半径作$\widehat{CE}$,交OB于E点.