题目内容
19．（1）用同一种特殊的多边形（如三个角都相等的等边三角形，四个角都相等的正方形等）能否铺满平面？有哪几种情况？（2）用同一种一般四边形能否铺满平面？说明理由．
分析 （1）根据平面图形镶嵌的条件：判断一种图形是否能够镶嵌，只要看一看拼在同一顶点处的几个角能否构成周角．若能构成360°，则说明能够进行平面镶嵌；反之则不能，即可得出答案；
（2）由镶嵌的条件知，在一个顶点处各个内角的和为360°时，就能镶嵌．根据任意一般四边形的内角和是360°，只要放在同一顶点的4个内角和为360°，即可得出答案．
解答 解：（1）用同一种正多边形镶嵌，能铺满平面，只有正方形，正六边形，等边三角形三种正多边形能镶嵌成一个平面图案，有三种情况；
（2）用同一种一般四边形能铺满平面；理由：
由镶嵌的条件知，在一个顶点处各个内角的和为360°时，就能镶嵌．
而任意四边形的内角和是360°，只要放在同一顶点的4个内角和为360°即可，故能铺满平面．
点评 此题考查了平面镶嵌的定义：用形状，大小完全相同的一种或几种平面图形进行拼接．彼此之间不留空隙，不重叠地铺成一片，这就是平面图形的镶嵌．判断一种或几种图形是否能够镶嵌，只要看一看拼在同一顶点处的几个角能否构成周角，若能构成360°，则说明能够进行平面镶嵌，反之则不能．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
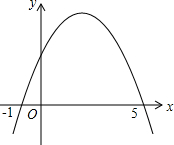已知一个二次函数，当x=1时，函数有最大值-6，且图象过点（2，-8）．
市“家乐福”超市购进一批20元/千克的绿色食品，如果以30元/千克销售，那么每天可售出400千克，由销售经验知，每天销售量y（千克）与销售单价x（元）（x≥30）存在如图所示的一次函数关系式．