题目内容
11.计算:(1)$\root{3}{\frac{1}{8}}$+$\sqrt{(-3)^{2}}$-$\frac{5}{2}$$\root{3}{-\frac{1}{125}}$
(2)|$\sqrt{3}$-$\sqrt{2}$|+|$\sqrt{3}$-2|-|$\sqrt{2}$-1|
分析 (1)直接利用立方根的性质以及二次根式的性质分别化简求出答案;
(2)直接利用绝对值的性质分析化简得出答案.
解答 解:(1)原式=$\root{3}{\frac{1}{8}}$+$\sqrt{(-3)^{2}}$-$\frac{5}{2}$$\root{3}{-\frac{1}{125}}$
=$\frac{1}{2}$+3-$\frac{5}{2}$×(-$\frac{1}{5}$)
=4;
(2)|$\sqrt{3}$-$\sqrt{2}$|+|$\sqrt{3}$-2|-|$\sqrt{2}$-1|
=$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$-($\sqrt{2}$-1)
=3-2$\sqrt{2}$.
点评 此题主要考查了实数运算,正确化简各数是解题关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
1.一个几何体的三视图如图所示,则这个几何体的侧面积是( )
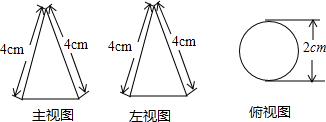

| A. | 4π | B. | 2π | C. | 4 | D. | π |
2.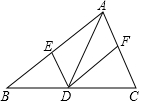 在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
 在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )| A. | 若AD⊥BC,则四边形AEDF是矩形 | |
| B. | 若AD垂直平分BC,则四边形AEDF是矩形 | |
| C. | 若BD=CD,则四边形AEDF是菱形 | |
| D. | 若AD平分∠BAC,则四边形AEDF是菱形 |
 公路施工中需要建设穿过小山的隧道DE,采用从两边同时施工的方法,甲工程队从D向E施工,乙工程队从E向D施工,为了使两工程队施工能在山中对接,需要保证A,D,E,C,在同一直线上.为此,在
公路施工中需要建设穿过小山的隧道DE,采用从两边同时施工的方法,甲工程队从D向E施工,乙工程队从E向D施工,为了使两工程队施工能在山中对接,需要保证A,D,E,C,在同一直线上.为此,在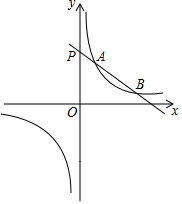 如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1),且与y轴交于点P.
如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1),且与y轴交于点P.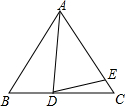 已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.