题目内容
【题目】⊙O的内接正三角形的边长记为a3,⊙O的内接正方形的边长记为a4,则![]() 等于_____.
等于_____.
【答案】![]()
【解析】
根据题意画出图形,设出圆的半径,再由正多边形及直角三角形的性质求解即可.
设圆的半径为r,
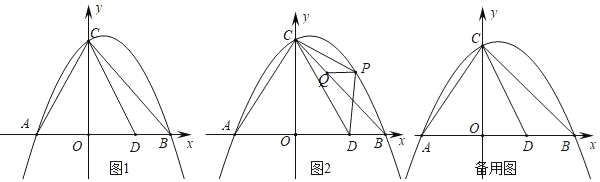
如图1,连接OB,OC,过点O作OD⊥BC于D,
∵△ABC内接于⊙O,
∴∠BOC=120°,OB=OC,
∴∠OBC=30°,
又∵∠BDO=90°,
∴BD=OB×cos30°=![]() ,
,
故BC=2BD=![]() ,
,
即a3=![]() ;
;
如图2,连接OB、OC,过O作OE⊥BC于E,
∵四边形ABCD内接于⊙O,
∴∠BOC=90°,OB=OC,
∴∠OBC=45°,
又∠BEO=90°,
∴△OBE是等腰直角三角形,OE=BE,
∴OB2=OE2+BE2=2BE2,
∴BE=![]() ,
,
∴BC=2BE=![]() ,
,
即a4=![]() ,
,
∴![]() ,
,
故答案为:![]() .
.


练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目