题目内容
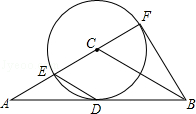 如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为D,直线AC交⊙C于点E、F,且CF=
如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为D,直线AC交⊙C于点E、F,且CF=| 1 |
| 2 |
(1)求∠ACB的度数;
(2)若AC=6,求BF的长.
考点:切线的性质
专题:计算题
分析:(1)连结CD,如图,根据切线的性质得CD⊥AB,再利用扥国药三角形的性质得到∠ACB=∠BCD,由于CF=
AC,CF=CD,则CD=
AC,于是根据含30度的直角三角形三边的关系得到∠A=30°,所以∠ACD=60°,于是可得∠ACB=120°;
(2)利用邻补角得到∠BCF=60°,则∠BCF=∠BCD,再证明△BCD≌△BCF得到∠BFC=∠BDC=90°,BF=BD,所以BF=AD,然后在Rt△ACD中根据含30度的直角三角形三边的关系可计算出AD,从而得到BF的长.
| 1 |
| 2 |
| 1 |
| 2 |
(2)利用邻补角得到∠BCF=60°,则∠BCF=∠BCD,再证明△BCD≌△BCF得到∠BFC=∠BDC=90°,BF=BD,所以BF=AD,然后在Rt△ACD中根据含30度的直角三角形三边的关系可计算出AD,从而得到BF的长.
解答:解:(1)连结CD,如图,
∵AB是⊙C的切线,
∴CD⊥AB,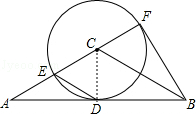
而CA=CB,
∴CD平分∠ACB,
即∠ACB=∠BCD,
∵CF=
AC,
而CF=CD,
∴CD=
AC,
∴∠A=30°,
∴∠ACD=60°,
∴∠ACB=2∠ACD=120°;
(2)∵∠BCF=180°-∠ACB=60°,
∴∠BCF=∠BCD,
在△BCD和△BCF中,
∴△BCD≌△BCF,
∴∠BFC=∠BDC=90°,BF=BD,
∴BF=AD,
在Rt△ACD中,∵∠A=30°,AC=6,
∴CD=
AC=3,
∴AD=
CD=3
,
∴BF=3
.
∵AB是⊙C的切线,
∴CD⊥AB,

而CA=CB,
∴CD平分∠ACB,
即∠ACB=∠BCD,
∵CF=
| 1 |
| 2 |
而CF=CD,
∴CD=
| 1 |
| 2 |
∴∠A=30°,
∴∠ACD=60°,
∴∠ACB=2∠ACD=120°;
(2)∵∠BCF=180°-∠ACB=60°,
∴∠BCF=∠BCD,
在△BCD和△BCF中,
|
∴△BCD≌△BCF,
∴∠BFC=∠BDC=90°,BF=BD,
∴BF=AD,
在Rt△ACD中,∵∠A=30°,AC=6,
∴CD=
| 1 |
| 2 |
∴AD=
| 3 |
| 3 |
∴BF=3
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了含30度的直角三角形三边的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一次函数y=kx+b,现分别从装有1,-2两张数字卡片的甲口袋和装有-1,2,3三张数字卡片的乙口袋中随机抽一张,甲口袋的卡片上的数字作k,乙口袋的卡片上的数字作b,则该一次函数的图象经过一、二、四象限的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数是二次函数的是( )
| A、y=2x+1 | ||
B、y=
| ||
| C、y=x2+2 | ||
D、y=
|
已知点A(1,y1),B(2,y2),C(-3,y3)都在反比例函数y=
(k>0)的图象上,则y1,y2,y3的大小关系是( )
| k |
| x |
| A、y3<y1<y2 |
| B、y1<y2<y3 |
| C、y2<y1<y3 |
| D、y3<y2<y1 |
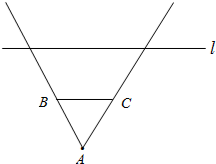 如图,小明同学站在离墙(BC)5米的A处,发现小强同学在离墙(BC)20米远且与墙平行的一条公路l上骑车,已知墙BC长为24米,小强骑车速度10米/秒,则小明看不见小强的时间为
如图,小明同学站在离墙(BC)5米的A处,发现小强同学在离墙(BC)20米远且与墙平行的一条公路l上骑车,已知墙BC长为24米,小强骑车速度10米/秒,则小明看不见小强的时间为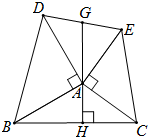 如图,AB=AD,AC=AE,∠BAD=∠CAE=90°.AH⊥BC于点H,HA的延长线交DE于G.求证:GD=GE.
如图,AB=AD,AC=AE,∠BAD=∠CAE=90°.AH⊥BC于点H,HA的延长线交DE于G.求证:GD=GE.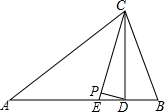 在△ABC中,∠A=38°,∠B=70°,CD⊥AB于点D,CE平分∠ACB,DP⊥CE于点P,求∠CDP的度数.
在△ABC中,∠A=38°,∠B=70°,CD⊥AB于点D,CE平分∠ACB,DP⊥CE于点P,求∠CDP的度数.