题目内容
把抛物线y=
x2平行移动，顶点移到（-3，-2），得到抛物线 ；如果顶点移到（2，3），那么得到抛物线 ．
| 1 |
| 12 |
考点：二次函数图象与几何变换
专题：
分析：平移不改变抛物线的开口方向与开口大小，即解析式的二次项系数不变，根据抛物线的顶点式可求抛物线解析式．
解答：解：∵原抛物线解析式为y=
x2，平移后抛物线顶点坐标为（-3，-2），
∴平移后的抛物线的表达式为：y=
（x+3）2-2．
同理，如果顶点移到（2，3），那么得到抛物线y=
（x-2）2+3．
故本题答案为：y=
（x+3）2-2，y=
（x-2）2+3．
| 1 |
| 12 |
∴平移后的抛物线的表达式为：y=
| 1 |
| 12 |
同理，如果顶点移到（2，3），那么得到抛物线y=
| 1 |
| 12 |
故本题答案为：y=
| 1 |
| 12 |
| 1 |
| 12 |
点评：本题考查了抛物线的平移与解析式变化的关系．关键是明确抛物线的平移实质上是顶点的平移，能用顶点式表示平移后的抛物线解析式．
练习册系列答案
相关题目
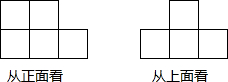如图所示的是由小立方体搭成的几何体从正面，上面看得到的平面图形，回答下列问题：