题目内容
(14分)如图,已知抛物线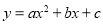 (
(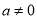 )与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
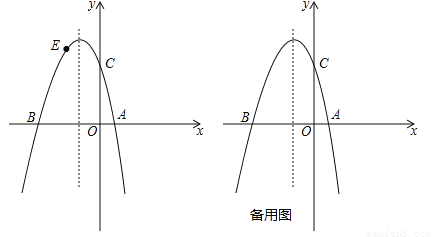
(1)求此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
(1);(2)当a=时,S四边形BOCE最大,且最大值为,此时,点E坐标为(,);(3)P(﹣1,1)或(﹣1,﹣2). 【解析】 试题分析:(1)将A、B两点的坐标代入抛物线的解析式中,即可求出二次函数的解析式; (2)过E作EF⊥x轴于F.设E(a,)(﹣3<a<0),则EF=,BF=a+3,OF=﹣a,∴S四边形BOCE==BF•EF+(OC+EF)•OF =,配方即可得出...
练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目


 B.
B. 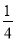 C.
C. 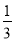 D.
D. 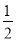
 的部分图象如图所示,则一元二次方程
的部分图象如图所示,则一元二次方程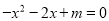 的解为:_____.
的解为:_____.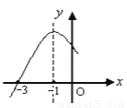
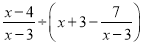 ,其中
,其中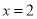 .
.