Question

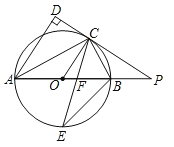
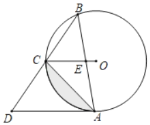
【题目】如图，已知⊙O是△ABC的外接圆，连接OC，过点A作AD∥OC，交BC的延长线于D，AB交OC于E，∠ABC＝45°．

(1)求证：AD是⊙O的切线；

(2)若AE＝，CE＝3．

①求⊙O的半径；

②求图中阴影部分的面积．

Answer 1

【答案】(1)证明见解析；(2)OC=4；(3)图中阴影部分的面积．

【解析】

（1）连接 ，根据圆周角定理可知 ，根据平行线的性质即可求出 ，从而可证AD是⊙O的切线

（2）①设 ，根据 ，可知 ，在中，根据勾股定理可知： ，即可求出半径的长；

②根据扇形面积公式以及三角形面积公式可求得答案。

解：(1)连接 ，如下图所示，

∵ ，

∴ ，

∵ ，

∴ ，

∵ 是⊙O的半径，

∴是⊙O的切线，

（2）①设 ，

∵ ，

∴ ，

由于 ，

在中，根据勾股定理可知：

∴ ，

∴ ，

∴ ；

② ，

，

∴图中阴影部分的面积．