Question

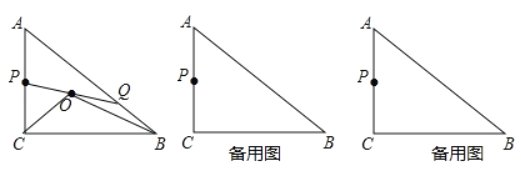
【题目】已知，如图Rt△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点P为AC的中点，Q从点A运动到B，点Q运动到点B停止，连接PQ，取PQ的中点O，连接OC，OB．

(1)若△ABC∽△APQ，求BQ的长；

(2)在整个运动过程中，点O的运动路径长_____；

(3)以O为圆心，OQ长为半径作⊙O，当⊙O与AB相切时，求△COB的面积．

Answer 1

【答案】(1)BQ=8.2cm；(2)5cm；(3)S△BOC＝.

【解析】

(1)根据得，从而得到的长即可求出的长；

（2）由点与点重合和点与点重合时，可以确定点的位置，再根据点位于上除端点外的任意一点时，由点是的中点，点是的中点可知是的中位线，从而得到点的运动轨迹是的 中位线，即线段，即可求得答案；

（3）连接，过点作 ，先证明得到 ，所以求得的值，且，再证明得到，求得的值，再根据即可求得答案；

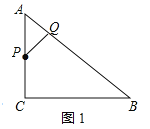
解：(1)如图1所示，

∵

∴

又∵点P为AC的中点，

∴

∵

∴ ，即

解之得：

则

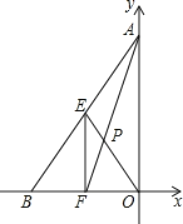
(2)如图2，

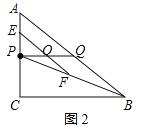
当点Q与点A重合时，点O位于点E的位置，

当点Q与点B重合时，点O位于点F的位置，

则EF是△APB的中位线，

∴EF∥AB，且EF＝AB＝5，

而当点Q位于AB上除端点外的任意一点时，

∵点O是PQ中点，点F是PB的中点，

∴OF是△PBQ的中位线，

∴OF∥BQ，

∴点O的运动轨迹是线段EF，

则点O的运动路径长是5cm；

故答案为：5cm．

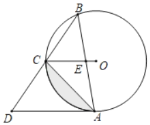
(3)如图3，连接 ，过点O作于点N，

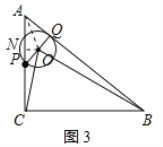
∵⊙O与AB相切，

∴ ，即 ，

∵

∴

∴ ，即

解之得：

则

∵

∴

又∵

∴，

∴ ，即 ，

解之得:

则