Question

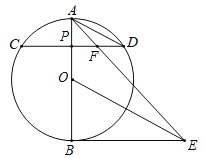
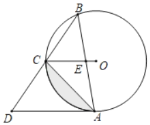
【题目】如图，已知是圆的直径，点是圆上一点，与过点的切线垂直，垂足为点，直线与的延长线相交于点,弦平分，交于点，连接

（1）求证：平分；

（2）求证：是等腰三角形；

（3）若，，求圆的半径长.

Answer 1

【答案】(1)证明见解析；(2)证明见解析；(3) 圆的半径为.

【解析】

（1）根据切线的性质得OC⊥DP，而AD⊥DP，则肯定判断OC∥AD，根据平行线的性质得∠DAC=∠OCA，加上∠OAC=∠OCA，所以∠OAC=∠DAC,即可求证.
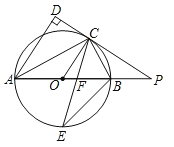
（2）根据圆周角定理由AB为圆O的直径得∠ACB=90°，则∠BCE=45°，再利用圆周角定理得∠BOE=2∠BCE=90°，则∠OFE+∠OEF=90°，易得∠CFP+∠OEF=90°，再根据切线的性质得到∠OCF+∠PCF=90°，而∠OCF=∠OEF，根据等角的余角相等得到∠PCF=∠CFP，于是可判断△PCF是等腰三角形；
（3）连结OE．由AB为 O的直径，得到∠ACB=90°，根据角平分线的定义得到∠BCE=45°，设圆O的半径为r，则OF=6-r，根据勾股定理列方程即可得到结论．

(1)证明：∵为圆的切线，

∴，

∵，

∴//,

∴，

∵

∴，

∴，

∴平分；

(2)证明：∵是圆的直径，

∴，

∵平分∠，

∴，

∴，

∴，

而，

∴，

∵，

∴,即，

而，

∴，

∴是等腰三角形；

(3)连结，

∵是圆的直径,

∴，

∵平分∠,

∴，

∴，即，

设圆的半径为，则，

在中,

∵，

∴，

解得，

当时,(符合题意)，

当时,(不合题意,舍去)，

∴圆的半径为.