题目内容
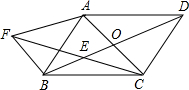 已知,如图,平行四边形ABCD的两条对角线相交于点O,E是BO的中点,过点B作AC的平行线,交CE的延长线于点F,连结BF.
已知,如图,平行四边形ABCD的两条对角线相交于点O,E是BO的中点,过点B作AC的平行线,交CE的延长线于点F,连结BF.(1)求证:FB=AO;
(2)当平行四边形ABCD满足什么条件时,四边形AFBO是菱形?证明你的结论.
考点:平行四边形的判定与性质,菱形的判定
专题:
分析:(1)如图,取BC的中点G.由三角形中位线定理易证EG=
BF=
OC;则由“有一组对边平行且相等的四边形为平行四边形”证得四边形AOBF为平行四边形.所以平行四边形的对边相等:FB=AO;
(2)若四边形AFBO是菱形,则OB=OA.故当平行四边形ABCD的对角线相等,即平行四边形ABCD是矩形时,四边形AFBO是菱形.
| 1 |
| 2 |
| 1 |
| 2 |
(2)若四边形AFBO是菱形,则OB=OA.故当平行四边形ABCD的对角线相等,即平行四边形ABCD是矩形时,四边形AFBO是菱形.
解答: 证明:(1)如图,取BC的中点G,连接EG.
证明:(1)如图,取BC的中点G,连接EG.
∵E是BO的中点,
∴EG是△BFC的中位线,
∴EG=
BF.
同理,EG=
OC,
∴BF=OC.
又∵点O是?ABCD的对角线交点,
∴AO=CO,
∴BF=AO.
又∵BF∥AC,即BF∥AO,
∴四边形AOBF为平行四边形,
∴FB=AO;
(2)当平行四边形ABCD是矩形时,四边形AFBO是菱形.理由如下:
∵平行四边形ABCD是矩形,
∴OA=OB,
∴平行四边形AFBO是菱形.
 证明:(1)如图,取BC的中点G,连接EG.
证明:(1)如图,取BC的中点G,连接EG.∵E是BO的中点,
∴EG是△BFC的中位线,
∴EG=
| 1 |
| 2 |
同理,EG=
| 1 |
| 2 |
∴BF=OC.
又∵点O是?ABCD的对角线交点,
∴AO=CO,
∴BF=AO.
又∵BF∥AC,即BF∥AO,
∴四边形AOBF为平行四边形,
∴FB=AO;
(2)当平行四边形ABCD是矩形时,四边形AFBO是菱形.理由如下:
∵平行四边形ABCD是矩形,
∴OA=OB,
∴平行四边形AFBO是菱形.
点评:本题考查了平行四边形的判定与性质以及菱形的判定,有利于学生思维能力的训练.涉及的知识点有:有一组邻边相等的平行四边形是菱形;矩形的对角线相等.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
下列六个数-π,-0.1,
,
,3.14,cos45°中无理数的个数为( )
| 1 |
| 2 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,一轮船沿正东方向匀速航行,在A地测得小岛P在北偏东30°方向,此船航行1h到达B地时,测得小岛P在北偏东15°方向.
如图,一轮船沿正东方向匀速航行,在A地测得小岛P在北偏东30°方向,此船航行1h到达B地时,测得小岛P在北偏东15°方向. 已知平行四边形ABCD,AB=3,AD=5.
已知平行四边形ABCD,AB=3,AD=5. 某衬衫厂,生产某品牌衬衫的成本价位50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍,批发价不低于55元.
某衬衫厂,生产某品牌衬衫的成本价位50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍,批发价不低于55元.