题目内容
如图，已知∠ABC的平分线与∠BCD的平分线交于点P，过点P分别向OA、OD做垂线，垂足是M、N．则点P考点：角平分线的性质
专题：
分析：过P作PH⊥BC于点H，则由条件可得到PM=PH=PN，根据角平分线的判定可知P在∠AOD的平分线上．
解答：
解：过P作PH⊥BC于点H，
∵BP、CP分别平分∠ABC和∠BCD，且PM⊥OA，PN⊥OD，
∴PM=PH=PN，
∴P在∠AOD的平分线上，
故答案为：在．
解：过P作PH⊥BC于点H，∵BP、CP分别平分∠ABC和∠BCD，且PM⊥OA，PN⊥OD，
∴PM=PH=PN，
∴P在∠AOD的平分线上，
故答案为：在．
点评：本题主要考查角平分线的性质和判定，掌握角平分线上的点到角两边的距离相等是解题的关键．
练习册系列答案
相关题目
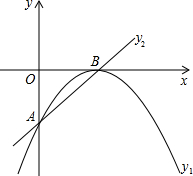二次函数y1=a（x-2）2的图象与直线y2交于A（0，-1），B（2，0）两点．（1）确定二次函数与直线AB的解析式．
（2）如图，分别确定当y1＜y2，y1=y2，y1＞y2时，自变量x的取值范围．
某工程需要在规定时间内完成，如果甲工程队单独做，恰好如期完成； 如果乙工程队单独做，则多用3天，现在甲、乙两队合做2天，剩下的由乙队单独做，恰好如期完成，求规定时间．如果设规定时间为x天，下面所列方程中正确的是（ ）
A、
| ||||||
B、
| ||||||
C、（
| ||||||
D、
|
如图，在直线l上求一点P，使PA=PB．不写作法，保留作图痕迹．