题目内容
10. 如图,已知⊙A过原点O且与x轴交于点C(6,0),与y轴交于点B(0,8),P为圆上第一象限的点,连结OP,PC,设过点O,C的抛物线的顶点为D,若存在以O,C,D为顶点的三角形与△OCP相似,则P点的坐标为($\frac{192}{25}$,$\frac{144}{25}$).
如图,已知⊙A过原点O且与x轴交于点C(6,0),与y轴交于点B(0,8),P为圆上第一象限的点,连结OP,PC,设过点O,C的抛物线的顶点为D,若存在以O,C,D为顶点的三角形与△OCP相似,则P点的坐标为($\frac{192}{25}$,$\frac{144}{25}$).
分析 如图,连接BC、PC,作PH⊥OC于H.因为D是抛物线的顶点,所以OD=CD,因为△OCP由△OCD相似,推出OC=PC,推出$\widehat{OC}$=$\widehat{PC}$,
推出∠CBO=∠CBP=∠POC,于tan∠POH=tan∠CBO=$\frac{OC}{BO}$=$\frac{3}{4}$=$\frac{PH}{OH}$,设PH=3k,OH=4k,在Rt△PCH中,根据PC2=PH2+CH2列出方程即可解决问题.
解答 解:如图,连接BC、PC,作PH⊥OC于H.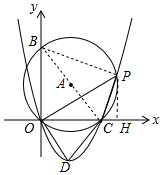
∵D是抛物线的顶点,
∴OD=CD,
∵△OCP由△OCD相似,
∴OC=PC,
∴$\widehat{OC}$=$\widehat{PC}$,
∴∠CBO=∠CBP=∠POC,
∵点C(6,0),点B(0,8),
∴OC=CP=6,OB=8,
∴tan∠POH=tan∠CBO=$\frac{OC}{BO}$=$\frac{3}{4}$=$\frac{PH}{OH}$,设PH=3k,OH=4k,
在Rt△PCH中,∵PC2=PH2+CH2,
∴62=(3k)2+(4k-6)2,
∴k=$\frac{48}{25}$,
∴OH=4k=$\frac{192}{25}$,PH=3k=$\frac{144}{25}$,
∴点P坐标为($\frac{192}{25}$,$\frac{144}{25}$).
故答案为($\frac{192}{25}$,$\frac{144}{25}$).
点评 本题考查抛物线由x轴的交点、锐角三角函数、相似三角形的判定和性质、勾股定理,圆周角定理等知识,解题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,属于中考填空题中的压轴题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
1.一个角的补角是这个角的余角的5倍,则这个角为( )
| A. | 22.5° | B. | 45° | C. | 67.5° | D. | 75° |
18.近似数2.30表示的准确数a的范围是( )
| A. | 2.295≤a<2.305 | B. | 2.25≤a<2.35 | C. | 2.295≤a≤2.305 | D. | 2.25<a≤2.35 |
15. 已知∠AOC=∠BOD=90°,∠AOB=170°,则∠DOC=( )
已知∠AOC=∠BOD=90°,∠AOB=170°,则∠DOC=( )
 已知∠AOC=∠BOD=90°,∠AOB=170°,则∠DOC=( )
已知∠AOC=∠BOD=90°,∠AOB=170°,则∠DOC=( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
19.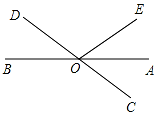 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOE的度数等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOE的度数等于( )
 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOE的度数等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOE的度数等于( )| A. | 145° | B. | 135° | C. | 35° | D. | 120° |
 如图,A、B、C、D在同一条直线上,AB=6,AD=$\frac{1}{3}$AB,CD=1,则BC=3.
如图,A、B、C、D在同一条直线上,AB=6,AD=$\frac{1}{3}$AB,CD=1,则BC=3. 如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为2$\sqrt{6}$.
如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为2$\sqrt{6}$.