题目内容
观察如下算式:
=
-
=1-
=
=
-
=
-
=
=
-
=
×(1-
)=
…
试计算:
(1)1+
+
+
…+
(2)
+
+
+
.
| 1 |
| 1×2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 6 |
| 2 |
| 6 |
| 1 |
| 6 |
| 1 |
| 1×3 |
| 1 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
试计算:
(1)1+
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 19×20 |
(2)
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 7×9 |
考点:规律型:数字的变化类
专题:
分析:由等式可以得出:
(1)根据分母是两个连续自然数的积,分子是1的分数可以拆成两个分子是1,分母是这两个自然数的分数的差即可;
(2)根据分母是两个连续奇数的积,分子是1的分数可以拆成两个分子是1,分母是这两个奇数的分数的差的
即可.
(1)根据分母是两个连续自然数的积,分子是1的分数可以拆成两个分子是1,分母是这两个自然数的分数的差即可;
(2)根据分母是两个连续奇数的积,分子是1的分数可以拆成两个分子是1,分母是这两个奇数的分数的差的
| 1 |
| 2 |
解答:解:(1)1+
+
+
…+
=1+1-
+
-
+
-
+…+
-
=2-
=1
;
(2)
+
+
+
=
×(1-
+
-
+
-
+
-
)
=
×
=
.
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 19×20 |
=1+1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 19 |
| 1 |
| 20 |
=2-
| 1 |
| 20 |
=1
| 19 |
| 20 |
(2)
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 7×9 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 9 |
=
| 1 |
| 2 |
| 8 |
| 9 |
=
| 4 |
| 9 |
点评:此题考查算式的变化规律,找出规律,利用规律解决问题.

练习册系列答案
相关题目
 如图,P是线段AB的黄金分割点(PB>PA),四边形ABCD、四边形PBEF都是正方形,且面积分别为S1、S2,四边形APMD、四边形APFN都是矩形,且面积分别为S3、S4,下列说法正确的是( )
如图,P是线段AB的黄金分割点(PB>PA),四边形ABCD、四边形PBEF都是正方形,且面积分别为S1、S2,四边形APMD、四边形APFN都是矩形,且面积分别为S3、S4,下列说法正确的是( )A、s2=
| ||||
| B、s2=s3 | ||||
C、s3=
| ||||
D、s4=
|
 如图,在三角形纸片ABC中,∠C=90°,AC=18,将∠A沿DE折叠,使点A与点B重合,折痕和AC交于点E,EC=5,则BC的长为( )
如图,在三角形纸片ABC中,∠C=90°,AC=18,将∠A沿DE折叠,使点A与点B重合,折痕和AC交于点E,EC=5,则BC的长为( ) 如图,点P在反比例函数y=
如图,点P在反比例函数y=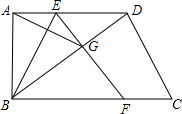 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,点E为底AD上一点,将△ABE沿直线BE折叠,点A落在梯形对角线BD上的G处,EG的延长线交直线BC于点F.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,点E为底AD上一点,将△ABE沿直线BE折叠,点A落在梯形对角线BD上的G处,EG的延长线交直线BC于点F.