题目内容
 如图,在矩形ABCD中,AB=10,CB=5,P,O分别是线段AC,AB上的动点,PO+PB的最小值为
如图,在矩形ABCD中,AB=10,CB=5,P,O分别是线段AC,AB上的动点,PO+PB的最小值为考点:轴对称-最短路线问题,矩形的性质
专题:
分析:作B关于AC的对称点B′,连结AB′,则N点关于AC的对称点N′在AB′上,这时,B到M到N的最小值等于B→M→N′的最小值,等于B到AB′的距离BH′.
解答: 解:作B关于AC的对称点B′,作B′O⊥OB于O,交AC于P.
解:作B关于AC的对称点B′,作B′O⊥OB于O,交AC于P.
连结AB′,则O点关于AC的对称点H′在AB′上,
∴∠AHB=∠AHB′=90°,BH=B′H,
∴AB′=AB,
∴∠AB′H=∠ABH.
这时,B到P到O的最小值等于B→P→H′的最小值,
等于B到AB′的距离BH′,
连结AB′和DC的交点E,
则S△ABE=
×10×5=25,
由对称知识,∠EAC=∠BAC=∠ECA,
所以EA=EC,令EA=x,则EC=x,ED=20-x,
在Rt△ADE中,
∵EA2=ED2+AD2,即x2=(10-x)2+52,
∴x=
,
∵S△ABE=
EA•BH′,
∴BH′=
=
=8.
在△BB′H′和△B′BQ中,
,
∴△BB′H′≌△B′BQ(AAS),
∴BH′=B′Q=8.
故答案为:8.
 解:作B关于AC的对称点B′,作B′O⊥OB于O,交AC于P.
解:作B关于AC的对称点B′,作B′O⊥OB于O,交AC于P.连结AB′,则O点关于AC的对称点H′在AB′上,
∴∠AHB=∠AHB′=90°,BH=B′H,
∴AB′=AB,
∴∠AB′H=∠ABH.
这时,B到P到O的最小值等于B→P→H′的最小值,
等于B到AB′的距离BH′,
连结AB′和DC的交点E,
则S△ABE=
| 1 |
| 2 |
由对称知识,∠EAC=∠BAC=∠ECA,
所以EA=EC,令EA=x,则EC=x,ED=20-x,
在Rt△ADE中,
∵EA2=ED2+AD2,即x2=(10-x)2+52,
∴x=
| 25 |
| 4 |
∵S△ABE=
| 1 |
| 2 |
∴BH′=
| 2S△ABE |
| EA |
| 25×2 | ||
|
在△BB′H′和△B′BQ中,
|
∴△BB′H′≌△B′BQ(AAS),
∴BH′=B′Q=8.
故答案为:8.
点评:本题考查的是轴对称-最短路线问题,考查轴对称的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,解答此题时作出B点关于直线AC对称的点B′是解答此题的关键.

练习册系列答案
相关题目
 如图,若直线y=kx+b经过A,B两点,直线y=mx经过A点,则关于x的不等式kx+b>mx的解集是
如图,若直线y=kx+b经过A,B两点,直线y=mx经过A点,则关于x的不等式kx+b>mx的解集是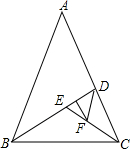 如图,顶角为36°的等腰三角形,其底边与腰的比是k,这样的三角形叫黄金三角形,已知腰长AB=1,△ABC为第一个黄金三角形,△BCD是第二个黄金三角形,△CDE是第三个黄金三角形,以此类推,第2006个黄金三角形的周长是
如图,顶角为36°的等腰三角形,其底边与腰的比是k,这样的三角形叫黄金三角形,已知腰长AB=1,△ABC为第一个黄金三角形,△BCD是第二个黄金三角形,△CDE是第三个黄金三角形,以此类推,第2006个黄金三角形的周长是