题目内容
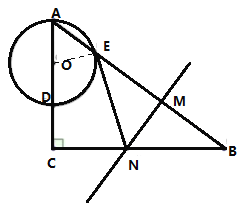
【题目】如图,在![]() 中,
中, ![]() , 在
, 在![]() ,上取一点
,上取一点![]() ,以
,以![]() 为直径作
为直径作![]() ,与
,与![]() 相交于点
相交于点![]() ,作线段
,作线段![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
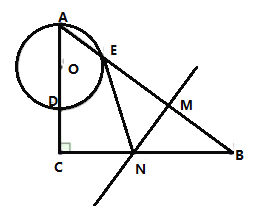
(1) 求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() 的半径为
的半径为![]() .求线段
.求线段![]() 与线段
与线段![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据题意,证出EN与OE垂直即可;
(2)求线段的长一般构造直角三角形,利用勾股定理来求解.在Rt△OEN、Rt△OCN△中,EN=ON-OE,ON=OC+CN,CN=4-EN代入可求EN;同理构造直角三角形Rt△AED、Rt△EDB、Rt△DCB,AE=AD-DE,DE=DB-BE,DB=CD+CB=1+4=17,代入求AE.
![]() 证明:连接
证明:连接![]()
![]() 是
是![]() 的垂直平分线
的垂直平分线
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 即
即![]()
![]() 是半径
是半径
![]() 是圆的切线
是圆的切线
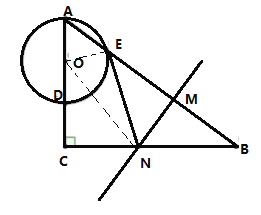
![]() 解:连接
解:连接![]()
设![]() 长为
长为![]() ,则
,则![]()
![]() ,圆的半径为
,圆的半径为![]()
![]()
![]()
![]()
解得![]() ,所以
,所以![]()
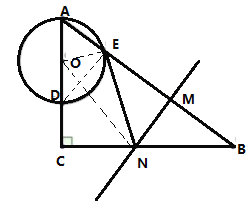
连接![]() 设
设![]()
![]()
∴AB=5,
∵AD是直径, ![]()
∴△ADE是直角三角形
则![]()
![]()
![]()
![]() 为直径,
为直径,
∴△DEB是直角三角形,
![]()
即(2-y)+(5-y) =17
解得![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目