题目内容
18．如果关于x的不等式$\frac{3x-a}{5}＜\frac{1-x}{2}$的解集为x＜2，求a的值．分析 解不等式求得x＜$\frac{5+2a}{11}$，由解集为x＜2得$\frac{5+2a}{11}$=2，解之即可得．
解答 解：去分母，得：2（3x-a）＜5（1-x），
去括号，得：6x-2a＜5-5x，
移项，得：6x+5x＜5+2a，
合并同类项，得：11x＜5+2a，
系数化为1，得：x＜$\frac{5+2a}{11}$，
由题意知$\frac{5+2a}{11}$=2，
解得：a=$\frac{17}{2}$．
点评 本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．
练习册系列答案
相关题目
8．
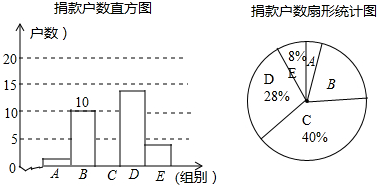某社区居民参加献爱心活动，为了解该社区居民捐款情况，对社区部分捐款户数进行分组统计，数据整理成如图所示的不完整统计图．已知A、B两组捐款户数直方图的高度比为1：5，请结合图中相关数据回答下列问题．
捐款分组统计表：
（1）求本次调查样本的容量和扇形统计图中A组对应扇形的圆心角度数．
（2）求出C组的频数，并补全直方图．
（3）若该社区有600户住户，请估计捐款不少于300元的户数是多少？
某社区居民参加献爱心活动，为了解该社区居民捐款情况，对社区部分捐款户数进行分组统计，数据整理成如图所示的不完整统计图．已知A、B两组捐款户数直方图的高度比为1：5，请结合图中相关数据回答下列问题．捐款分组统计表：
| 组别 | 捐款额（x）元 |
| A | 10≤x＜100 |
| B | 100≤x＜200 |
| C | 200≤x＜300 |
| D | 300≤x＜400 |
| E | x≥400 |
（2）求出C组的频数，并补全直方图．
（3）若该社区有600户住户，请估计捐款不少于300元的户数是多少？
6．一个多边形的内角和与它的外角和的比为5：2，则这个多边形的边数为（ ）
| A． | 8 | B． | 7 | C． | 6 | D． | 5 |
13．若$\sqrt{3x+1}$在实数范围内有意义，则x的取值范围是（ ）
| A． | x$＞\frac{1}{3}$ | B． | x≥$\frac{1}{3}$ | C． | x≥-$\frac{1}{3}$ | D． | x＞-$\frac{1}{3}$ |
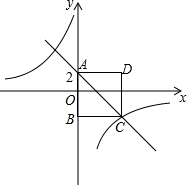如图，四边形ABCD为正方形．点A的坐标为（0，2），点B的坐标为（0，-3）．反比例函数y=$\frac{k}{x}$图象经过点C，一次函数y=ax+b的图象经过点A、C．