题目内容
 如图,在△ABC中,∠ABC=90°,AB=BC,过点B作BD⊥AC于D,BE平分∠DBC,交AC于E,过点A作AF⊥BE于G,交BC于F,交BD于H.则下列结论中:
如图,在△ABC中,∠ABC=90°,AB=BC,过点B作BD⊥AC于D,BE平分∠DBC,交AC于E,过点A作AF⊥BE于G,交BC于F,交BD于H.则下列结论中:①AF平分∠BAC;②AB=AE;③BH=HF;④DH=CF;⑤AC=AB+BH.
正确结论的序号是
考点:全等三角形的判定与性质,角平分线的性质,等腰直角三角形
专题:
分析:首先证明∠HBG=∠HAD,再证明∠GBF=∠BAF,再根据∠GBF=∠HBG可得∠HAD=∠BAF,进而得到结论;过点D作KD∥FC交AF于K,所以
=
=
,然后可以证出进而得到FC=2KD,再证明∠DKH=∠DHK得到KD=HD,进而得到FC=2HD,再根据全等三角形的判定和性质证明其他选项即可.
| KD |
| FC |
| AD |
| AC |
| 1 |
| 2 |
解答:解:∵BD⊥AC,AF⊥BE,
∴∠ADH=∠HGB=90°.
∵∠BHG=∠AHD,
∴∠HBG=∠HAD.
∵∠ABC=∠FGB=90°,
∴∠BAF+∠AFB=90°,
∠GBF+∠AFB=90°.
∴∠GBF=∠BAF.
∵BE平分∠DBC,
∴∠GBF=∠HBG.
∴∠HAD=∠BAF.
即 AF平分∠BAC故①正确;
∵BG⊥AG,BG平分∠DBC,
∴BH=BF,
∵∠HBF=45°,
∴△BHF不是等边三角形,
∴BH≠HF,故③不正确;
∵AB=BC,∠ABC=90°,
∴∠C=∠BAC=45°,
∵BE平分∠DBC,
∴∠DBE=∠CBE,
∴∠AEB=∠ABE,
在△ABH和△AEG中,
,
∴△ABH≌△AEG,
∴AB=AE故②正确;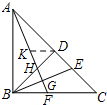
②∵在Rt△ABC中,∠ABC=90°,∠BAC=45°,
∴∠C=∠BAC=45°,
∴AB=BC.
∵BD⊥AC,
∴AD=DC=
AC.
过点D作KD∥FC交AF于K,
∴
=
=
.
∴FC=2KD,
∵BE平分∠DBC,BE⊥AF,
∴∠DBE=∠EBF,∠HGB=∠FGB=90°.
∴∠BFH=∠BHF.
∴∠BHF=∠DHK.
∴∠BFH=∠DHK.
∵KD∥BC,
∴∠DKH=∠BFH.
∴∠DKH=∠DHK.
∴KD=HD.
∴FC=2HD故④错误;
∵AB=AE,AC=AE+CE,
∴AC=AB+CE,
而CE≠BF,
∴AC≠AB+BF,
故⑤错误,
故答案为:①②.
∴∠ADH=∠HGB=90°.
∵∠BHG=∠AHD,
∴∠HBG=∠HAD.
∵∠ABC=∠FGB=90°,
∴∠BAF+∠AFB=90°,
∠GBF+∠AFB=90°.
∴∠GBF=∠BAF.
∵BE平分∠DBC,
∴∠GBF=∠HBG.
∴∠HAD=∠BAF.
即 AF平分∠BAC故①正确;
∵BG⊥AG,BG平分∠DBC,
∴BH=BF,
∵∠HBF=45°,
∴△BHF不是等边三角形,
∴BH≠HF,故③不正确;
∵AB=BC,∠ABC=90°,
∴∠C=∠BAC=45°,
∵BE平分∠DBC,
∴∠DBE=∠CBE,
∴∠AEB=∠ABE,
在△ABH和△AEG中,
|
∴△ABH≌△AEG,
∴AB=AE故②正确;

②∵在Rt△ABC中,∠ABC=90°,∠BAC=45°,
∴∠C=∠BAC=45°,
∴AB=BC.
∵BD⊥AC,
∴AD=DC=
| 1 |
| 2 |
过点D作KD∥FC交AF于K,
∴
| KD |
| FC |
| AD |
| AC |
| 1 |
| 2 |
∴FC=2KD,
∵BE平分∠DBC,BE⊥AF,
∴∠DBE=∠EBF,∠HGB=∠FGB=90°.
∴∠BFH=∠BHF.
∴∠BHF=∠DHK.
∴∠BFH=∠DHK.
∵KD∥BC,
∴∠DKH=∠BFH.
∴∠DKH=∠DHK.
∴KD=HD.
∴FC=2HD故④错误;
∵AB=AE,AC=AE+CE,
∴AC=AB+CE,
而CE≠BF,
∴AC≠AB+BF,
故⑤错误,
故答案为:①②.
点评:此题主要考查了等腰直角三角形的性质、全等三角形的判定和性质以及平行线分线段成比例定理,关键是证明KD=HD和MD=HD.此题综合性较强,找准角之间的相等关系是解决此题的难点.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
下列图中,∠1与∠2是对顶角的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在△ABC中,AB的垂直平分线交AC于点E,已知△ABC和△BCE的周长分别是8和5,则AD=
如图,在△ABC中,AB的垂直平分线交AC于点E,已知△ABC和△BCE的周长分别是8和5,则AD=