题目内容
8．若等腰三角形的周长为26cm，一边为11cm，则另外两边为7.5cm，7.5cm或11cm，4cm．分析 题中给出了周长和一边长，而没有指明这边是否为腰长，则应该分两种情况进行分析求解．
解答 解：①当11cm为腰长时，则腰长为11cm，底边=26-11-11=4cm，因为11+4＞11，所以能构成三角形；
②当11cm为底边时，则腰长=（26-11）÷2=7.5cm，因为7.5+7.5＞11，所以能构成三角形．
故答案为：7.5cm，7.5cm或11cm，4cm
点评 此题主要考查等腰三角形的性质及三角形三边关系的综合运用，关键是利用三角形三边关系进行检验．
练习册系列答案
名校课堂系列答案
相关题目
19．某校研究性学习小组在学习二次根式$\sqrt{{a}^{2}}$=|a|之后，研究了如下四个问题，其中错误的是（ ）
| A． | 在a＞1的条件下化简代数式a+$\sqrt{{a}^{2}-2a+1}$的结果为2a-1 | |
| B． | 当a+$\sqrt{{a}^{2}-2a+1}$的值恒为定值时，字母a的取值范围是a≤1 | |
| C． | a+$\sqrt{{a}^{2}-2a+1}$的值随a变化而变化，当a取某个数值时，上述代数式的值可以为$\frac{1}{2}$ | |
| D． | 若$\sqrt{{a}^{2}-2a+1}$=（$\sqrt{a-1}$）2，则字母a必须满足a≥1 |
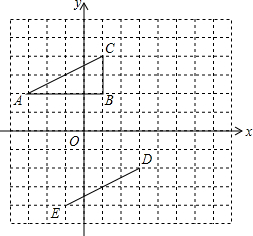在平面直角坐标系中，△ABC的顶点坐标是A（-3，2），B（1，2），C（1，4）．线段DE的端点坐标是D（3，-2），E（-1，-4）．