题目内容
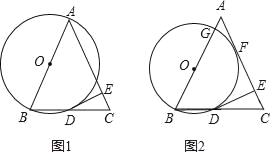
【题目】如图①,![]() 是
是![]() 外一点,过点
外一点,过点![]() 做
做![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .若
.若![]() ,则点
,则点![]() 叫做
叫做![]() 的切角点.
的切角点.
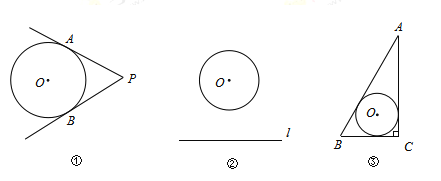
(1)如图②,![]() 的半径是1,点O到直线
的半径是1,点O到直线![]() 的距离为2.若点
的距离为2.若点![]() 是
是![]() 的切角点,且点
的切角点,且点![]() 在直线
在直线![]() 上,请用尺规作出点
上,请用尺规作出点![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
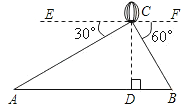
(2)如图③,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的内切圆.若点
的内切圆.若点![]() 是
是![]() 的切角点,且点
的切角点,且点![]() 在
在![]() 的边上,求
的边上,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() 的长为
的长为![]() 或2
或2
【解析】
(1)作图见详解,(2)根据特殊直角三角形性质求出三角形的三边长和内角度数,分类讨论找到P点位置,根据特殊的角度即可解题.
解:(1)如图,点![]() 即为所求.
即为所求.

(2)![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,



![]() ,
,![]() .
.
![]() 是
是![]() 的内切圆,
的内切圆,
设![]() 、
、![]() 、
、![]() 分别与
分别与![]() 相切于点
相切于点![]() ,
,
∴OD⊥AC,ON⊥BC,OM⊥AB,BM=BN,CN=CD,AM=AD.
![]() ,
,![]() 四边形
四边形![]() 为矩形.
为矩形.
![]() ,
,![]() 矩形
矩形![]() 为正方形.
为正方形.
设![]() 的半径为
的半径为![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
![]() .
.
即![]() .
.
解得![]() .
.
![]() ,
,![]() .
.
如图①,![]() ,且
,且![]() 、
、![]() 与
与![]() 分别相切于点
分别相切于点![]() 、
、![]() ,
,
![]() 点
点![]() 是
是![]() 的切角点,即点
的切角点,即点![]() 与点
与点![]() 重合,此时
重合,此时![]() .
.
如图②,若![]() 的切角点
的切角点![]() 在线段
在线段![]() 上,
上,![]() 与
与![]() 相切于点
相切于点![]() .
.
由切角点的概念知![]() .
.
连接![]() ,有
,有![]() .
.
![]() 是
是![]() 的半径,
的半径,![]() .
.
![]() ,
,![]() .
.
![]() .
.
![]() ,
,![]() .
.
![]() .
.
如图③,若![]() 的切角点
的切角点![]() 在线段
在线段![]() 上.
上.
与上一种情况类似计算可得![]() .
.
则![]() .
.
综上,![]() 的长为
的长为![]() 或2.
或2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目