题目内容
19．在△ABC中，DE∥BC，$\frac{AD}{AB}=\frac{1}{2}$，且S△ABC=8cm2，那么S△ADE=2cm2．分析 由DE∥BC，可判定△ADE∽△ABC，然后由相似三角形面积比等于相似比的平方，求得答案．
解答 解：∵DE∥BC，
∴△ADE∽△ABC，
∴S△ADE：S△ABC=（$\frac{AD}{AB}$）2，
∵$\frac{AD}{AB}=\frac{1}{2}$，
∴S△ADE：S△ABC=1：4，
∵S△ABC=8cm2，
∴S△ADE=2cm2．
故答案为：2．
点评 此题考查了相似三角形的判定与性质．注意证得△ADE∽△ABC是解此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
9．下列条件中，不能判定△ABC是等腰三角形的是（ ）
| A． | a=3，b=3，c=4 | B． | a：b：c=2：3：4 | C． | ∠B=50°，∠C=80° | D． | ∠A：∠B：∠C=1：1：2 |
如图，在△ABC中，DE∥BC交AB、AC于点D、E，AE=3，AC=5，DE=4，那么BC=$\frac{20}{3}$．
7．
已知：如图，正方形网格中，∠AOB如图放置，则cos∠AOB的值为（ ）
已知：如图，正方形网格中，∠AOB如图放置，则cos∠AOB的值为（ ）| A． | $\frac{{2\sqrt{5}}}{5}$ | B． | 2 | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{5}}}{5}$ |
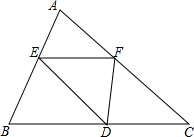如图，△ABC中，E、F、D分别是AB、AC、BC上的点，且满足$\frac{AE}{EB}=\frac{AF}{FC}=\frac{2}{3}$，则S△ABC：S△EFD=25：6．
如图，AC=AD，线段AB经过线段CD的中点E，求证：BC=BD．
如图，在边长为6$\sqrt{2}$的正方形ABCD中，E是AB边上一点，G是AD延长线上一点，BE=DG，连接EG，过点C作EG的垂线CH，垂足为点H，连接BH，BH=8．有下列结论：