题目内容
【题目】如图,矩形OABC中,A(6,0)、C(0,![]() )、D(0,
)、D(0,![]() ),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
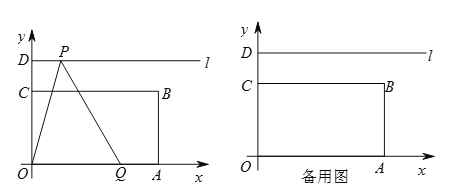
(1)①点B的坐标是 ;
②当点Q与点A重合时,点P的坐标为 ;
(2)设点P的横坐标为x,△OPQ与矩形OABC的重叠部分的面积为S,试求S与x的函数关系式及相应的自变量x的取值范围.
【答案】(1)①(6,![]() ),②(3,
),②(3,![]() );(2)
);(2)
【解析】
(1)①由四边形OABC是矩形,根据矩形的性质,即可求得点B的坐标;②由正切函数,即可求得∠CAO的度数,③由三角函数的性质,即可求得点P的坐标;
(2)分别从当0≤x≤3时,当3<x≤5时,当5<x≤9时,当x>9时去分析求解即可求得答案.
解:(1)①∵四边形OABC是矩形,
∴AB=OC,OA=BC,
∵A(6,0)、C(0,2![]() ),
),
∴点B的坐标为:(6,2![]() );
);
②如图1:当点Q与点A重合时,过点P作PE⊥OA于E,

∵∠PQO=60°,D(0,3![]() ),
),
∴PE=3![]() ,
,
∴AE=![]() ,
,
∴OE=OA-AE=6-3=3,
∴点P的坐标为(3,3![]() );
);
故答案为:①(6,2![]() ),②(3,3
),②(3,3![]() );
);
(2)①当0≤x≤3时,
如图,OI=x,IQ=PItan60°=3,OQ=OI+IQ=3+x;
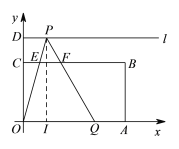
由题意可知直线l∥BC∥OA,
∴![]() ,
,
∴EF=![]()
此时重叠部分是梯形,其面积为:
S梯形=![]() (EF+OQ)OC=
(EF+OQ)OC=![]() (3+x)
(3+x)
∴![]() .
.
当3<x≤5时,如图

AQ=OIIOOA=x36=x3
AH=![]() (x3)
(x3)
S=S梯形﹣S△HAQ=S梯形﹣![]() AHAQ=
AHAQ=![]() (3+x)﹣
(3+x)﹣![]()
∴![]() .
.
③当5<x≤9时,如图

∵CE∥DP
∴![]()
∴![]()
∴![]()
![]()
S=![]() (BE+OA)OC=
(BE+OA)OC=![]() (12﹣
(12﹣![]() )
)
∴![]() .
.
④当x>9时,如图

∵AH∥PI
∴![]()
∴![]()
∴![]()
S=![]() OAAH=
OAAH=![]() .
.
综上: .
.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
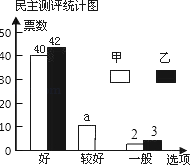
英才点津系列答案【题目】在校园歌手大赛中,甲、乙两位同学的表现分外突出,现场A、B、C、D、E、F六位评委的打分情况以及随机抽取的50名同学的民意调查结果分别如下统计表和不完整的条形统计图:(说明:随机抽取的50名同学每人必须从“好”、“较好”、“一般”中选一票投给每个选手)
A | B | C | D | E | F | |
甲 | 89 | 97 | 90 | 93 | 95 | 94 |
乙 | 89 | 92 | 90 | 97 | 94 | 94 |
(1)a= ,六位评委对乙同学所打分数的中位数是 ,并补全条形统计图;
(2)学校规定评分标准如下:去掉评委评分中最高和最低分,再算平均分并将平均分与民意测评分按2:3计算最后得分.求甲、乙两位同学的最后得分.(民意测评分=“好”票数×2+“较好”票数×1+“一般”票数×0)
【题目】小尧用“描点法”画二次函数![]() 的 图像,列表如下:
的 图像,列表如下:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
y | … | 5 | 0 | -3 | -4 | -3 | 0 | -5 | … |
(1)由于粗心,小尧算错了其中的一个 y值,请你指出这个算错的y值所对应的 x = ;
(2)在图中画出这个二次函数![]() 的图像;
的图像;
(3)当 y≥5 时,x 的取值范围是 .