Question

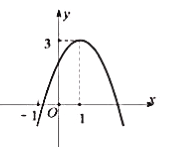
【题目】如图，抛物线y=-x2+mx的对称轴为直线x=2，若关于x的-元二次方程-x2+mx-t=0 (t为实数)在l<x<3的范围内有解，则t的取值范围是( )

A.-5<t≤4 B.3<t≤4 C.-5<t<3 D.t>-5

Answer 1

【答案】B

【解析】

先利用抛物线的对称轴方程求出m得到抛物线解析式为y=-x2+4x，配方得到抛物线的顶点坐标为（2，4），再计算出当x=1或3时，y=3，结合函数图象，利用抛物线y=-x2+4x与直线y=t在1＜x＜3的范围内有公共点可确定t的范围．

∵ 抛物线y=-x2+mx的对称轴为直线x=2，

∴，

解之：m=4，

∴y=-x2+4x，

当x=2时，y=-4+8=4，

∴顶点坐标为(2，4)，

∵ 关于x的-元二次方程-x2+mx-t=0 (t为实数)在l<x<3的范围内有解，

当x=1时，y=-1+4=3，

当x=2时，y=-4+8=4，

∴ 3<t≤4，

故选：B