题目内容
某商店经销一种销售成本为每千克40元的水产品;据市场分析,若按每千克50元销售,一个月能售出500千克,销售单价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,请你回答以下问题:
(1)应涨价多少元时获得的利润最大,最大利润是多少?
(2)商店想在售价为多少情况下,使得月利润达到8000元.
(1)应涨价多少元时获得的利润最大,最大利润是多少?
(2)商店想在售价为多少情况下,使得月利润达到8000元.
考点:二次函数的应用
专题:
分析:(1)设销售单价定为每千克x元,获得利润为w元,则可以根据成本,求出每千克的利润.以及按照销售价每涨1元,月销售量就减少10千克,可求出销量.从而得到总利润关系式,求最值;
(2)根据“销售单价每涨1元,月销售量就减少10千克”,可知:月销售量=500-(销售单价-50)×10.由此可得出售价为a元/千克时的月销售量,然后根据利润=每千克的利润×销售的数量来求出月销售利润.
(2)根据“销售单价每涨1元,月销售量就减少10千克”,可知:月销售量=500-(销售单价-50)×10.由此可得出售价为a元/千克时的月销售量,然后根据利润=每千克的利润×销售的数量来求出月销售利润.
解答:解:(1)设销售单价定为每千克x元,获得利润为w元,则:
w=(x-40)[500-(x-50)×10],
=(x-40)(1000-10x),
=-10x2+1400x-40000,
=-10(x-70)2+9000,
∴当x=70时,利润最大为9000元.
则涨价为70-50=20(元).
答:应涨价20元时获得的利润最大,最大利润是9000元;
(2)设当销售单价定为每千克a元时,月销售量为:[500-(a-50)×10]=(1000-10a)千克.
每千克的销售利润是:(a-40)元,
则(a-40)(1000-10a)=8000,
解得:a1=60,a2=80,
答:月销售利润达到8000元销售单价应定为60元或80元.
w=(x-40)[500-(x-50)×10],
=(x-40)(1000-10x),
=-10x2+1400x-40000,
=-10(x-70)2+9000,
∴当x=70时,利润最大为9000元.
则涨价为70-50=20(元).
答:应涨价20元时获得的利润最大,最大利润是9000元;
(2)设当销售单价定为每千克a元时,月销售量为:[500-(a-50)×10]=(1000-10a)千克.
每千克的销售利润是:(a-40)元,
则(a-40)(1000-10a)=8000,
解得:a1=60,a2=80,
答:月销售利润达到8000元销售单价应定为60元或80元.
点评:本题主要考查了二次函数的应用,能正确表示出月销售量是解题的关键.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角α为30°,测得C
如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角α为30°,测得C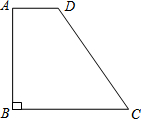 如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,tanC=
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,tanC=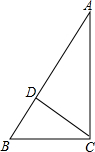 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,BC=3,AC=4,求AB、CD的长.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,BC=3,AC=4,求AB、CD的长.