题目内容
20.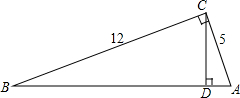 如图,CD是Rt△ABC斜边AB上的高,AC=5,BC=12.求tanA,sinB,cos∠ACD.
如图,CD是Rt△ABC斜边AB上的高,AC=5,BC=12.求tanA,sinB,cos∠ACD.
分析 利用勾股定理求得AB,tanA,sinB,cos∠ACD,进一步利用锐角三角函数的意义求得答案即可.
解答 解:在Rt△ABC中,AC=5,BC=12,
AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=13,
CD=$\frac{BC×AC×2}{AB}$=$\frac{120}{13}$,
tanA=$\frac{BC}{AC}$=$\frac{12}{5}$,
sinB=$\frac{AC}{AB}$=$\frac{5}{13}$,
cos∠ACD=$\frac{CD}{AC}$=$\frac{12}{13}$.
点评 此题考查解直角三角形,掌握勾股定理和锐角三角函数的意义是解决问题的关键.

练习册系列答案
相关题目
9.据报道,截至2014年12月,我国网民规模达649000000人,请将数据649000000用科学记数法表示为( )
| A. | 6.5×107 | B. | 6.49×108 | C. | 6.49×109 | D. | 6.49×1010 |
10.cos45°的值为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
 如图,D、E分别在△ABC的边上AC、AB上,请你添加一个条件∠ABC=∠ADE(答案不唯一)使得△ADE∽△ABC.
如图,D、E分别在△ABC的边上AC、AB上,请你添加一个条件∠ABC=∠ADE(答案不唯一)使得△ADE∽△ABC.
 如图,将由线段组成的两边∠ACB沿O点旋转,使A点到D点.
如图,将由线段组成的两边∠ACB沿O点旋转,使A点到D点.