题目内容
12. 如图,在三角形ABC中,AB∥DE,AD⊥BC,∠BAC=90°,与∠DAC相等的角(不包括∠DAC本身)有( )
如图,在三角形ABC中,AB∥DE,AD⊥BC,∠BAC=90°,与∠DAC相等的角(不包括∠DAC本身)有( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 先根据∠BAC=90°得出∠BAD+∠DAC=90°,再由AD⊥BC可知∠B+∠BAD=90°,故∠B=∠DAC,再由AB∥DE可知∠B=∠CDE,由此可得出结论.
解答 解:∵∠BAC=90°,
∴∠BAD+∠DAC=90°.
∵AD⊥BC,
∴∠B+∠BAD=90°,
∴∠B=∠DAC.
∵AB∥DE,
∴∠B=∠CDE=∠DAC.
故选C.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
相关题目
7.把方程2x+3y-1=0改写成含x的式子表示y的形式为( )
| A. | $y=\frac{1}{3}(2x-1)$ | B. | $y=\frac{1}{3}(1-2x)$ | C. | y=3(2x-1) | D. | y=3(1-2x) |
4. 如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )
如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )
 如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )
如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )| A. | 同位角相等,两直线平行 | |
| B. | 内错角相等,两直线平行 | |
| C. | 同旁内角互补,两直线平线 | |
| D. | 如果两条直线都和第三条直线平行,那么这两条直线平行 |
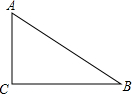 如图,在△ABC中,∠C=90°,那么点A到BC的距离是AC的长度,点B到AC的距离是BC的长度,点A,B两点的距离是AB的长度,三个距离最短的是AC,理由:垂线段最短.
如图,在△ABC中,∠C=90°,那么点A到BC的距离是AC的长度,点B到AC的距离是BC的长度,点A,B两点的距离是AB的长度,三个距离最短的是AC,理由:垂线段最短. 某校学生来自甲、乙、丙三个地区,其人数比为2:7:3,如图所示的扇形图表示上述分布情况,则∠AOB=60°.
某校学生来自甲、乙、丙三个地区,其人数比为2:7:3,如图所示的扇形图表示上述分布情况,则∠AOB=60°.