题目内容
15. 如图,在正方形ABCD中∠DAE=25°,AE交对角线BD于E点,那么∠BEC等于( )
如图,在正方形ABCD中∠DAE=25°,AE交对角线BD于E点,那么∠BEC等于( )| A. | 45° | B. | 60° | C. | 70° | D. | 75° |
分析 首先证明△AED≌△CED,即可证明∠ECD=∠DAE=25°,从而求得∠BEC,再根据三角形内角和定理即可求解.
解答 解:在△AED和△CED中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADE=∠CDE}\\{DE=DE}\end{array}\right.$,
∴△AED≌△CED,
∴∠ECD=∠DAE=25°,
又∵在△DEC中,∠CDE=45°,
∴∠CED=180°-25°-45°=110°,
∴∠BEC=180°-110°=70°.
故选:C.
点评 此题主要考查了正方形的性质,正确理解,证明△AED≌△CED是解题的关键.

练习册系列答案
相关题目
6.若$\frac{3a+1}{(a+3)(a-1)}$=$\frac{m}{a+3}$+$\frac{n}{a-1}$,则( )
| A. | m=-3,n=1 | B. | m=3,n=-1 | C. | m=3,n=1 | D. | m=2,n=1 |
20.若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-1 | B. | k>-1且k≠0 | C. | k<1 | D. | k<1且k≠0 |
7.下列运算正确的是( )
| A. | -22÷(-2)2=1 | B. | ${({-2\frac{1}{3}})^3}=-8\frac{1}{27}$ | C. | $-5÷\frac{1}{3}×\frac{3}{5}=-25$ | D. | -32+(-3)2=0 |
4. 某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
 某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )| A. | 873名 | B. | 1115名 | C. | 485名 | D. | 1067名 |
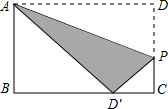 如图,矩形ABCD中,AB=8,BC=10,点P在矩形的边DC上由点D向点C运动,沿直线AP翻折三角形ADP,使点D恰好落在BC边上.求DP的长和三角形ADP与矩形重叠(阴影)部分的面积.
如图,矩形ABCD中,AB=8,BC=10,点P在矩形的边DC上由点D向点C运动,沿直线AP翻折三角形ADP,使点D恰好落在BC边上.求DP的长和三角形ADP与矩形重叠(阴影)部分的面积. 如图,一辆小汽车从小山脚下的A点直线行驶15分钟到达山顶的B点,已知小汽车的平均速度为40千米/时,小山的高度BC约为6000米,求小山的坡比.
如图,一辆小汽车从小山脚下的A点直线行驶15分钟到达山顶的B点,已知小汽车的平均速度为40千米/时,小山的高度BC约为6000米,求小山的坡比.